수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
앞서 불균형 데이터 처리의 중요성과 간단한 방법들에 대해 알아보았습니다.
임계값(threshold)를 조정하는 법, 그리고 랜덤 오버샘플링(Random Oversampling), 랜덤 언더샘플링(Random Undersampling)을 보았습니다.
이번엔 또 다른 접근법으로 소수 클래스의 샘플을 증가시키는 SMOTE(Synthetic Minority Over sampling Technique), ADASYN(Adaptive Synthetic Sampling)에 대해 알아보겠습니다.
간단하게, SMOTE는 소수 클래스의 샘플을 인위적으로 생성하여 데이터 세트의 균형을 개선하는 방법으로, 랜덤 오버샘플링과 같이 분포안에서 랜덤하게 추가 데이터를 생성하는게 아닌 샘플 간의 선형 보간을 통해 새로운 샘플을 생성합니다.
ADASYN은 SMOTE의 발전형으로, 다수 클래스 샘플 근처에 더 많은 합성 샘플을 생성함으로써 학습 과정에서 모델이 더 어려운 샘플에 더 많은 주의를 기울이도록 합니다.
이 두 기법의 기본 원리와 주요 차이점에 대해 간략하게 소개해보도록 합시다.
📌 SMOTE
SMOTE는 소수 클래스 내의 샘플들 사이에 존재하는 패턴을 학습하여 새로운 합성된 샘플들을 생성합니다.
수식으로 한번 살펴보겠습니다.
1. 샘플 선택 : 소수 클래스에서 샘플 $x_i$를 무작위로 선택합니다.
2. 이웃 찾기 : k-최근접 이웃(knn)을 사용하여 $x_i$의 이웃 중 하나의 샘플 $x_n$을 선택합니다.
3. 샘플 생성 : $x_i$와 $x_n$ 사이를 선형 보간하여 새로운 샘플을 생성합니다. 선형 보간이 어렵게 들릴 수도 있지만 단순히, $x_i$와 $x_n$의 차이에 0~1사이의 난수를 곱하여 $x_i$와 곱함으로써 두 샘플 사이에 새로운 샘플을 생성하는 것입니다.
수식은 아래와 같겠네요
$$x_{new} = x_i + \lambda \times (x_n - x_i)$$
그림과 같이 본다면 아래와 같습니다. 첫 번째 그림은 k=1로 설정하여 이웃을 한개만 보았을 때, 두 번째 그림은 k=3으로 성정하여 이웃을 세개 보았을 때입니다.
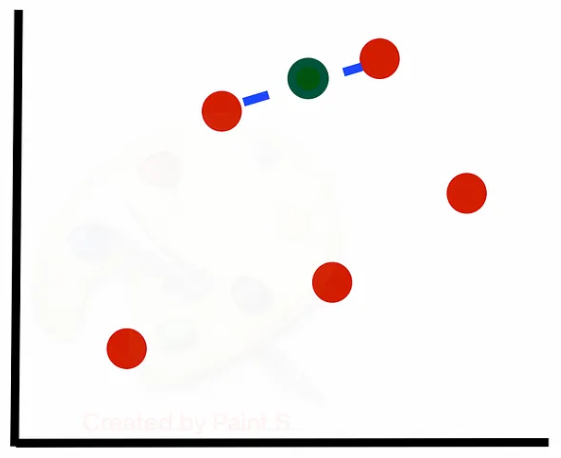
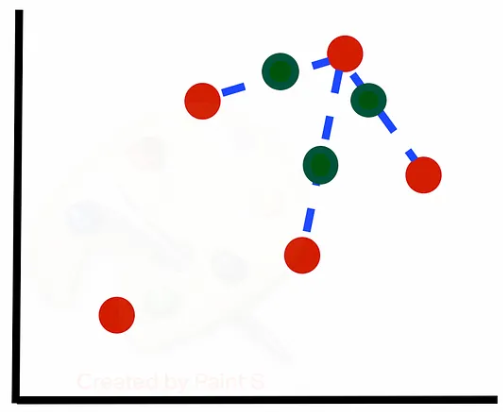
◼️ 한계
SMOTE가 이렇게 소수 클래스를 더 잘 인식하도록 해주지만, 이 기법은 소수 클래스의 이상치를 과도하게 증가시킬 수 있습니다. 또한 데이터 복잡성에 따라 적절한 knn 이웃 개수를 정하는 것이 어려울 수 있습니다.
◼️ with python
우선 파이썬의 mask_classification을 이용하여 불균형 데이터를 생성하겠습니다.
쉬운 시각화를 위해 feature의 수는 5개로 설정하고, feature1과 feature2를 이용한 2d 산점도를 보겠습니다.
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
# 인위적인 불균형 데이터셋 생성
X, y = make_classification(n_samples=500, n_features=5, n_informative=2,
n_redundant=2, n_clusters_per_class=1,
weights=[0.90, 0.10], flip_y=0, random_state=42)
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], label='Class 0', alpha=0.5)
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], label='Class 1', alpha=0.5)
plt.title('Imbalanced Dataset Visualization')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()각각 클래스 1이 50개, 클래스 0이 450개가 되도록 생성하였습니다.
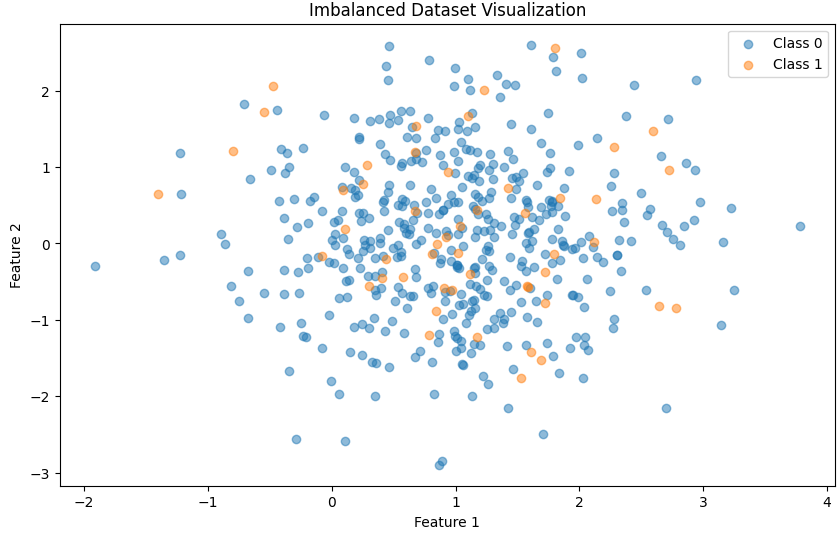
이후, 일반적인 ROS를 사용해보면
from imblearn.over_sampling import RandomOverSampler
# 랜덤 오버샘플링 수행
rus = RandomOverSampler(random_state=42)
X_res, y_res = rus.fit_resample(X, y)
plt.figure(figsize=(10, 6))
plt.scatter(X_res[y_res == 0][:, 0], X_res[y_res == 0][:, 1], label='Class 0', alpha=0.5)
plt.scatter(X_res[y_res == 1][:, 0], X_res[y_res == 1][:, 1], label='Class 1', alpha=0.5)
plt.title('Imbalanced Dataset Visualization with ROS')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()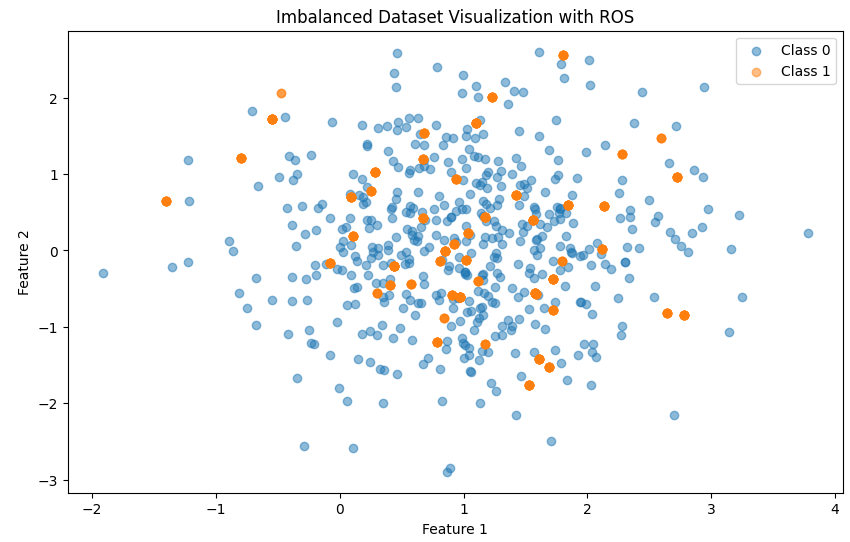
자 보시면, 소수 클래스인 클래스 1의 점 색이 진해진 것을 볼 수 있습니다. 이렇게 일반적인 ROS는 소수 클래스의 분포안에서 샘플을 추출하는 것이기 때문에 데이터 수가 많아지기만 할 뿐인 것을 볼 수 있습니다.
그렇다면 SMOTE를 사용해보죠.
from imblearn.over_sampling import SMOTE
# SMOTE 적용
sm = SMOTE(random_state=42)
X_sm, y_sm = sm.fit_resample(X, y)
plt.figure(figsize=(10, 6))
plt.scatter(X_sm[y_sm == 0][:, 0], X_sm[y_sm == 0][:, 1], label='Class 0', alpha=0.5)
plt.scatter(X_sm[y_sm == 1][:, 0], X_sm[y_sm == 1][:, 1], label='Class 1', alpha=0.5)
plt.title('Imbalanced Dataset Visualization with SMOTE')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()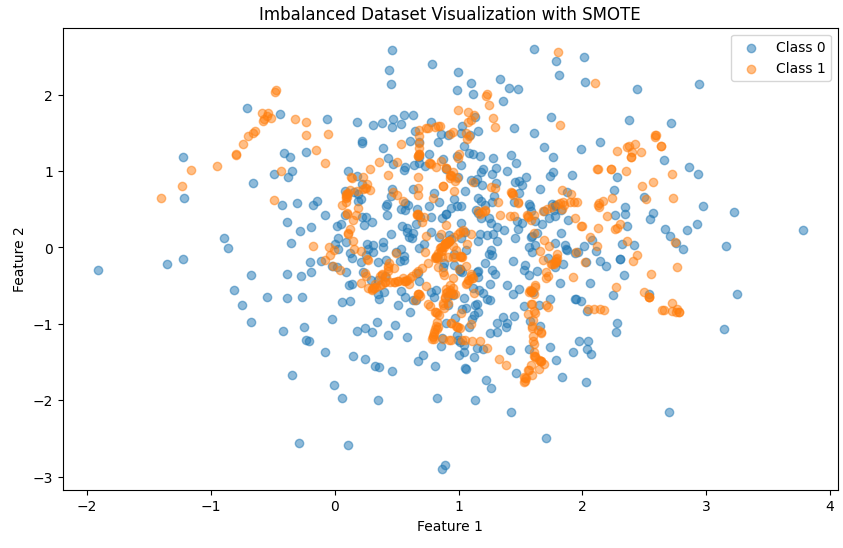
이렇게 단순 추출이 아닌 샘플들의 선형 보간을 통해 이루어 지기 때문에 샘플들 사이사이에 새로운 데이터들이 생긴것을 볼 수 있습니다.
📌 Adasyn
Adasyn은 SMOTE의 발전된 형태로, Adasyn 또한 소수 클래스 데이터의 샘플을 합성하여 증가시킵니다. 하지만 SMOTE와 달리 각 소수 클래스 샘플이 다수 클래스 샘플과의 경계에 얼마나 가까운지에 따라 샘플을 생성하는 비율을 동적으로 조정합니다.
쉽게 설명하면 SMOTE와 같이 소수 클래스 데이터와 그 데이터에서 가장 가까운 k개의 소수 클래스 데이터중 무작위로 선택된 데이터 사이의 직성상에 가상의 소수 클래스 데이터를 만드는 방법인데 다수 클래스가 많이 분포해 있는 주변에 더 많은 소수 클래스 샘플을 생성하는 것 입니다.
위에서 다수 클래스 샘플과의 경계와 얼마나 가까운지에 따라 샘플을 생성하는 비율을 조정한다고 하였는데, 이는 각 관측치마다 생성하는 샘플의 수가 다르다는 것입니다. 가중치를 이용하여 합성 샘플의 수를 결정하는데, 이 가중치는 knn 범위내로 들어오는 다수 클래스의 개수에 비례하도록 설정하는 것입니다.
이렇게 설정하는 이유는? 범위내에 다수 클래스의 개수가 많을 수록 훈련시키기 어렵기 때문에 이러한 어려운 관측치에 집중하는 것입니다.
수식과 함께 본다면
1. 이웃 계산 : 각 소수 클래스 샘플 $x_i$에 대해 knn을 계산하여, 다수 클래스 샘플이 얼마나 가까운지를 결정한다.
2. 생성 비율 결정 : 각 소수 클래스 샘플 $x_i$에 대해, 다수 클래스 이웃의 비율에 비례하여 합성 샘플을 생성할 비율 $r_i$를 계산.
$$r_i = \dfrac{\Delta_i}{\sum_{j=1}^n \Delta_i}$$
여기서 $\Delta_i$는 $x_i$의 knn 이웃 중 다수 클래스에 속하는 샘플의 수를 나타내며, n은 소수 클래스 샘플의 총 수이다.
3. 샘플 생성 : 이후 (다수 클래스 데이터 수 - 소수 클래스 데이터 수)를 위에서 구한 비율에 곱해줍니다. 이에 반올림된 정수 값 만큼 각 소수 클래스 데이터 주변에 SMOTE 방식으로 생성합니다.
◼️ 한계
SMOTE에 비해 분류기가 더 어려운 영역에서 더 잘 학습되로록 합니다. 하지만 이 역시 이상치에 민감할 수 있으며, knn의 이웃 수를 선택하는 것이 중요합니다.
바로 코드와 함께 살펴 봅시다.
◼️ with python
from imblearn.over_sampling import ADASYN
# ADASYN 적용
ad = ADASYN(random_state=42)
X_ad, y_ad = ad.fit_resample(X, y)
plt.figure(figsize=(10, 6))
plt.scatter(X_ad[y_ad == 0][:, 0], X_ad[y_ad == 0][:, 1], label='Class 0', alpha=0.5)
plt.scatter(X_ad[y_ad == 1][:, 0], X_ad[y_ad == 1][:, 1], label='Class 1', alpha=0.5)
plt.title('Imbalanced Dataset Visualization with ADASYN')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()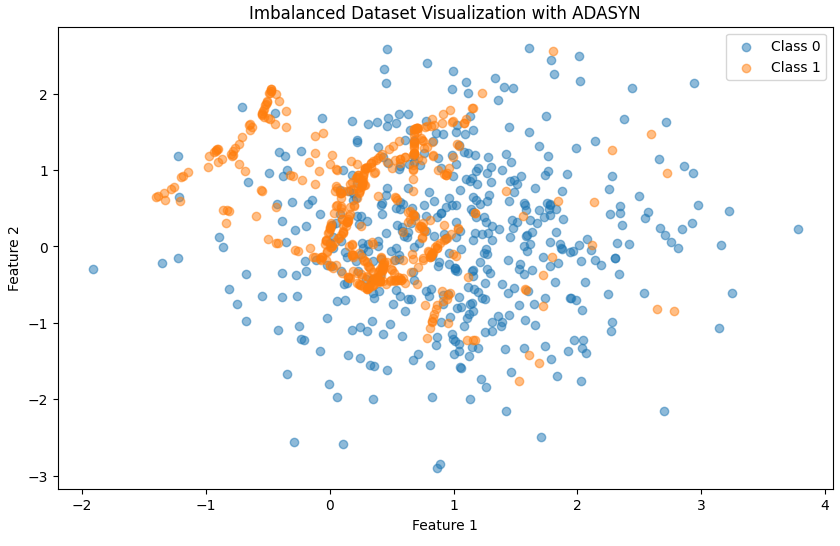
SMOTE와 차이를 보시면 SMOTE와 같은 경우에는 전체적으로 고르게 분포된 합성 샘플을 생성했지만, ADASYN의 다수 클래스가 많이 밀집해있는 중앙 부근에 합성 샘플을 다수 생성한 것을 볼 수 있습니다.
📌 성능 비교
간단한 모델로 성능 비교를 해보죠.로지스틱 회귀를 사용했고, 각 파라미터는 default 값을 사용했습니다. 그렇기에 정확한 성능은 아니지만 이들의 차이 정도 보면 좋겠습니다! 코드는 생략하고 결과를 본다면
----- ROS -----
Accuracy: 0.87
Precision: 0.4583333333333333
Recall (Sensitivity): 1.0
F1 Score: 0.6285714285714286----- SMOTE -----
Accuracy: 0.89
Precision: 0.5
Recall (Sensitivity): 1.0
F1 Score: 0.6666666666666666----- ADASYN -----
Accuracy: 0.84
Precision: 0.4074074074074074
Recall (Sensitivity): 1.0
F1 Score: 0.5789473684210525
ADASYN의 경우 ROS보다 좋지 못한 성능을 보였네요, 하지만 하이퍼 파라미터 조정에 따라 달라질 수 있고 실제 데이터에 적용했을 시 다른 결과를 얻을 수 있습니다.
예시로 보여준 것 뿐입니다!
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 부분 의존성 플롯(Partial Dependence Plot, PD) 그리고 개별 조건부 평균 플롯(Individual Conditional Expectation Plot, ICE) (1) | 2024.02.27 |
|---|---|
| Calibration Plot 과 성능 확인 (0) | 2024.02.27 |
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
