수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
불균형 데이터(Imbalaned Data)는 데이터 마이닝 세계에서 생각보다 흔히 마주치는 도전 과제이다.
예를 들면, 자살 예측 혹은 질병 예측과 같은 부분에서 흔하다. 자살 시도 혹은 자살 생각을 하는 이들을 비교적 많지 않기에 자살 생각이 있다는 Y = 1인 사람이 30명 없다는 Y = 0인 사람이 300명이 있는 경우이다.
이 경우, 모델을 적합할 때 자살 생각이 없다는 300명의 데이터의 패턴을 더 많이 학습하기 때문에 자살 생각을 예측하기 쉽지 않다.
이렇게 예측 모델링에서 클래스 간 불균형은 모델의 학습 능력에 큰 영향을 미칠 수 있으며, 이를 해결하기 위한 전략이 필요하다.
본 글에서는 가장 간단한 방법으로 임계값(Threshold)를 조정하는 방법을 소개하려고 한다. 아마 머신러닝에 관심이 깊은 사람은 들어봤을 것 같습니다.
📌 임계값 조정
임계값 조정은 데이터 처리 단계가 아닌 모델을 적합 한뒤에 적용하는 방법이다. 모델의 예측 성능을 최적화 하기 위해 예측 확률의 임계값을 조정하는 기법이다.
흔히 모델을 이용하여 레이블을 예측할 때 예측 확률 0.5를 기준으로 1 or 0으로 나뉘게 된다. 하지만 실제 분석에서 불균형 데이터셋의 경우 이러한 0.5를 기준으로 선택하는 것이 최적의 선택이 아닐 수 있다.
불균형 데이터의 경우 소수 클래스로 분류될 확률이 0.1~0.3과 같이 매우 낮은 확률을 가질 수 있기 때문이다. 그래서 임계값을 0.5가 아닌 0.2와 같이 연구자가 직접 설정해주는 방법이다.
이렇게 임계값을 조정함으로써, 모델의 민감도와 특이도 간의 균형을 조정하고 소수 클래스에 대한 모델의 예측력을 개선할 수 있다.
쉽게 그림으로 표현한다면 아래와 같은 느낌이다.

📌 With Python
파이썬 코드와 함께 보자. 사이킷런의 imbalnced-learn 패키지에 있는 함수를 활용하여 900개의 0과 100개의 1이 있는 불균형 데이터를 만들었고, feature는 총 20개 입니다.
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from collections import Counter
# 인위적인 불균형 데이터셋 생성
X, y = make_classification(n_samples=1000, n_features=20, n_informative=r,
n_redundant=3, n_clusters_per_class=2,
weights=[0.90, 0.10], flip_y=0, random_state=42)
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
plt.hist(y, bins=[-0.5, 0.5, 1.5], rwidth=0.6, color='skyblue', edgecolor='black')
plt.xticks([0, 1], ['0', '1'])
plt.title('Distribution of Target Classes in Breast Cancer Dataset')
plt.xlabel('Class')
plt.ylabel('Frequency')
plt.show()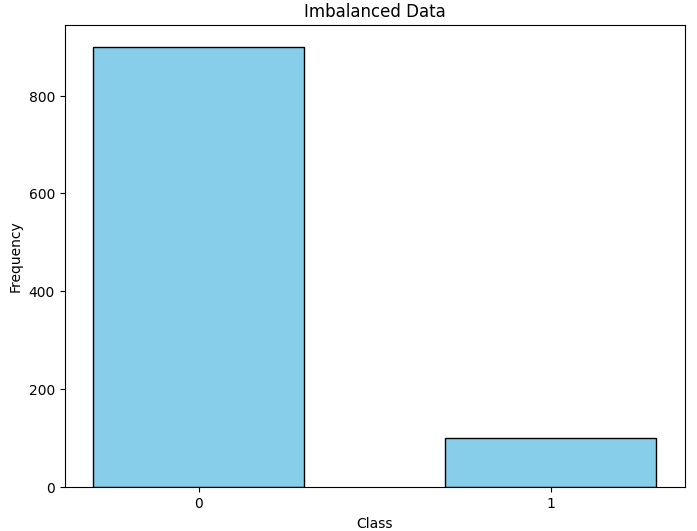
이를 통해 간단한 분류를 해봅시다. 간단한 모델인 로지스틱 회귀를 사용해보겠습니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
logistic = LogisticRegression(random_state = 42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
lo_model = logistic.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
y_pred = lo_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[181 0]
[ 17 2]]
Accuracy: 0.915
Precision: 1.0
Recall (Sensitivity): 0.10526315789473684
F1 Score: 0.1904761904761905
혼동행렬과 성능 지표를 보면 정확도 자체는 0.89로 높지만 정밀도와 민감도 그리고 F1 score에서 보듯 매우 낮은 성능을 보이는 것을 볼 수 있습니다. 불균형 데이터로 인해 대부분의 클래스가 0으로 분류된 것입니다.
1로 분류될 확률의 최댓값과 최소값을 확인해보면 아래와 같이 최대 0.78 최소 0.002가 나오는 것을 볼 수 있습니다.
y_scores = lo_model.predict_proba(X_test)[:, 1]
print(max(y_scores))
print(min(y_scores))0.7840787244842714
0.002438672720768426
그럽 임계값을 조정해가면서 분류 성능을 확인해보죠. 각 임계값에 대한 정밀도와 재현율을 그래프로 확인해보겠습니다.
from sklearn.metrics import precision_recall_curve
# 다양한 임계값에 대한 정밀도와 재현율 계산
precisions, recalls, thresholds = precision_recall_curve(y_test, y_scores)
# 임계값에 따른 정밀도와 재현율 시각화
plt.figure(figsize=(10, 6))
plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
plt.xlabel("Threshold")
plt.legend(loc="upper left")
plt.ylim([0,1])
plt.title("Precision and Recall by Threshold")
plt.show()

대략 임계값 0.26정도에서 타협을 본다고 해봅시다.
이 0.26값을 기준으로 0과 1로 레이블을 분류하였을 때 혼돌행렬과 성능 지표는 아래와 같습니다.
(원래는 또 다른 테스트 데이터 세트를 이용해야합니다!!! 우리가 테스트 데이터를 임계값이라는 새로운 하이퍼파라미터를 조정하는데 쓴것과 같기 때문에 일반화가 어렵습니다.)
threshold = 0.26 # 예시 임계값
y_pred_custom = (y_scores >= threshold).astype(int)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred_custom)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred_custom)
precision = precision_score(y_test, y_pred_custom)
recall = recall_score(y_test, y_pred_custom)
f1 = f1_score(y_test, y_pred_custom)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[171 10]
[ 12 7]]
Accuracy: 0.89
Precision: 0.4117647058823529
Recall (Sensitivity): 0.3684210526315789
F1 Score: 0.3888888888888889
보시면 정확도는 조금 내려갔지만 나머지 성능 지표는 조금 오른 것을 볼 수 있습니다. 얼마 오르지 못했는데 왜 중요하느냐?? 이것은 분류 문제에 따라 다릅니다. 만약 자살 시도를 예측할 경우 자살 시도를 하지 않는 것을 예측하는 것 보다 시도를 할 경우를 예측하는 경우가 매우 중요한 문제이기 때문에 1%라도 성능을 높이기 위함입니다.
본 예시에서는 만든 데이터를 사용했기 때문에 실제 성능은 크게 높아지지 않았지만, 실제 데이터의 경우 다를 가능성이 충분히 존재합니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
|---|---|
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
불균형 데이터(Imbalaned Data)는 데이터 마이닝 세계에서 생각보다 흔히 마주치는 도전 과제이다.
예를 들면, 자살 예측 혹은 질병 예측과 같은 부분에서 흔하다. 자살 시도 혹은 자살 생각을 하는 이들을 비교적 많지 않기에 자살 생각이 있다는 Y = 1인 사람이 30명 없다는 Y = 0인 사람이 300명이 있는 경우이다.
이 경우, 모델을 적합할 때 자살 생각이 없다는 300명의 데이터의 패턴을 더 많이 학습하기 때문에 자살 생각을 예측하기 쉽지 않다.
이렇게 예측 모델링에서 클래스 간 불균형은 모델의 학습 능력에 큰 영향을 미칠 수 있으며, 이를 해결하기 위한 전략이 필요하다.
본 글에서는 가장 간단한 방법으로 임계값(Threshold)를 조정하는 방법을 소개하려고 한다. 아마 머신러닝에 관심이 깊은 사람은 들어봤을 것 같습니다.
📌 임계값 조정
임계값 조정은 데이터 처리 단계가 아닌 모델을 적합 한뒤에 적용하는 방법이다. 모델의 예측 성능을 최적화 하기 위해 예측 확률의 임계값을 조정하는 기법이다.
흔히 모델을 이용하여 레이블을 예측할 때 예측 확률 0.5를 기준으로 1 or 0으로 나뉘게 된다. 하지만 실제 분석에서 불균형 데이터셋의 경우 이러한 0.5를 기준으로 선택하는 것이 최적의 선택이 아닐 수 있다.
불균형 데이터의 경우 소수 클래스로 분류될 확률이 0.1~0.3과 같이 매우 낮은 확률을 가질 수 있기 때문이다. 그래서 임계값을 0.5가 아닌 0.2와 같이 연구자가 직접 설정해주는 방법이다.
이렇게 임계값을 조정함으로써, 모델의 민감도와 특이도 간의 균형을 조정하고 소수 클래스에 대한 모델의 예측력을 개선할 수 있다.
쉽게 그림으로 표현한다면 아래와 같은 느낌이다.

📌 With Python
파이썬 코드와 함께 보자. 사이킷런의 imbalnced-learn 패키지에 있는 함수를 활용하여 900개의 0과 100개의 1이 있는 불균형 데이터를 만들었고, feature는 총 20개 입니다.
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from collections import Counter
# 인위적인 불균형 데이터셋 생성
X, y = make_classification(n_samples=1000, n_features=20, n_informative=r,
n_redundant=3, n_clusters_per_class=2,
weights=[0.90, 0.10], flip_y=0, random_state=42)
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
plt.hist(y, bins=[-0.5, 0.5, 1.5], rwidth=0.6, color='skyblue', edgecolor='black')
plt.xticks([0, 1], ['0', '1'])
plt.title('Distribution of Target Classes in Breast Cancer Dataset')
plt.xlabel('Class')
plt.ylabel('Frequency')
plt.show()
이를 통해 간단한 분류를 해봅시다. 간단한 모델인 로지스틱 회귀를 사용해보겠습니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
logistic = LogisticRegression(random_state = 42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
lo_model = logistic.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
y_pred = lo_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[181 0]
[ 17 2]]
Accuracy: 0.915
Precision: 1.0
Recall (Sensitivity): 0.10526315789473684
F1 Score: 0.1904761904761905
혼동행렬과 성능 지표를 보면 정확도 자체는 0.89로 높지만 정밀도와 민감도 그리고 F1 score에서 보듯 매우 낮은 성능을 보이는 것을 볼 수 있습니다. 불균형 데이터로 인해 대부분의 클래스가 0으로 분류된 것입니다.
1로 분류될 확률의 최댓값과 최소값을 확인해보면 아래와 같이 최대 0.78 최소 0.002가 나오는 것을 볼 수 있습니다.
y_scores = lo_model.predict_proba(X_test)[:, 1]
print(max(y_scores))
print(min(y_scores))0.7840787244842714
0.002438672720768426
그럽 임계값을 조정해가면서 분류 성능을 확인해보죠. 각 임계값에 대한 정밀도와 재현율을 그래프로 확인해보겠습니다.
from sklearn.metrics import precision_recall_curve
# 다양한 임계값에 대한 정밀도와 재현율 계산
precisions, recalls, thresholds = precision_recall_curve(y_test, y_scores)
# 임계값에 따른 정밀도와 재현율 시각화
plt.figure(figsize=(10, 6))
plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
plt.xlabel("Threshold")
plt.legend(loc="upper left")
plt.ylim([0,1])
plt.title("Precision and Recall by Threshold")
plt.show()

대략 임계값 0.26정도에서 타협을 본다고 해봅시다.
이 0.26값을 기준으로 0과 1로 레이블을 분류하였을 때 혼돌행렬과 성능 지표는 아래와 같습니다.
(원래는 또 다른 테스트 데이터 세트를 이용해야합니다!!! 우리가 테스트 데이터를 임계값이라는 새로운 하이퍼파라미터를 조정하는데 쓴것과 같기 때문에 일반화가 어렵습니다.)
threshold = 0.26 # 예시 임계값
y_pred_custom = (y_scores >= threshold).astype(int)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred_custom)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred_custom)
precision = precision_score(y_test, y_pred_custom)
recall = recall_score(y_test, y_pred_custom)
f1 = f1_score(y_test, y_pred_custom)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[171 10]
[ 12 7]]
Accuracy: 0.89
Precision: 0.4117647058823529
Recall (Sensitivity): 0.3684210526315789
F1 Score: 0.3888888888888889
보시면 정확도는 조금 내려갔지만 나머지 성능 지표는 조금 오른 것을 볼 수 있습니다. 얼마 오르지 못했는데 왜 중요하느냐?? 이것은 분류 문제에 따라 다릅니다. 만약 자살 시도를 예측할 경우 자살 시도를 하지 않는 것을 예측하는 것 보다 시도를 할 경우를 예측하는 경우가 매우 중요한 문제이기 때문에 1%라도 성능을 높이기 위함입니다.
본 예시에서는 만든 데이터를 사용했기 때문에 실제 성능은 크게 높아지지 않았지만, 실제 데이터의 경우 다를 가능성이 충분히 존재합니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
|---|---|
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
