수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
저번 포스팅에서 불균형 데이터에 대한 접근법으로 임계값 조정을 확인하였습니다.
불균형 데이터(Imbalanced Data) 접근법 : 임계값(threshold) 조정
불균형 데이터(Imbalaned Data)는 데이터 마이닝 세계에서 생각보다 흔히 마주치는 도전 과제이다. 예를 들면, 자살 예측 혹은 질병 예측과 같은 부분에서 흔하다. 자살 시도 혹은 자살 생각을 하는
datanovice.tistory.com
임계값 조정법은 모델을 적합한 이후에 성능을 확인 한 후 적용하는 방법이었습니다. 이번엔 오버 샘플링과 언더 샘플링입니다.
매우 간단한 방법으로,
오버 샘플링(over sampling)은 소수 클래스의 데이터를 다수 클래스만큼 가상 데이터를 만드는 접근법이며,
언더 샘플링(under sampling)은 다수 클래스의 데이터를 소수 클래스만큼 데이터를 제거하는 접근법입니다.
왜 불균형 데이터를 다루는 것이 중요한지는 위 임계값 조정 포스팅에 다루었으니 한 번씩 확인해주시면 감사하겠습니다!
📌 랜덤 오버샘플링
랜덤 오버샘플링은 소수 클래스의 샘플을 무작위로 복제하여, 소수 클래스의 빈도를 인위적으로 증가시킵니다.
좀 더 수학적으로 본다면 소수 클래스의 확률 분포인(y = 1이 소수라면) $P(x|y=1)$에서 추가 샘플을 추출하는 과정으로 볼 수 있겠죠.
물론 이론적으로 모델이 소수 클래스의 패턴을 더 잘 확인하고 학습할 수 있게 합니다만.. 정해진 분포 안에서 새로운 데이터를 추출하기 때문에 모델이 과적합될 위험이 있습니다.
📌 랜덤 언더샘플링
랜덤 언더샘플링은 다수 클래스의 샘플을 무작위로 제거하여, 클래스 간의 불균형을 줄이는 기법입니다.
이 역시 수학적으로 본다면 다수 클래스 확률 분포 $P(x|y=0)$에서 일부 샘플을 제거하는 과정으로 볼 수 있죠.
이 또한 이론적으로 소수 클래스와 다수 클래스 사이의 경계를 더 명확히 만들어 모델이 학습하기 좋게 만듭니다.
하지만, 언더 샘플링은 다수 클래스의 샘플을 제거하는 만큼 데이터의 정보를 잃는 위험이 있습니다. 주어진 데이터를 잃게 만드는 것은 빅데이터 시대에 큰 단점이라고 볼 수 있습니다. 때문에 언더 샘플링을 사용할 때는 중요한 정보의 손실을 최소화하는 것이 중요할 것입니다.
📌 with python
이번엔 파이썬과 함께 확인해보겠습니다. 이번에도 저번 포스팅과 같이 랜덤한 불균형 데이터를 생성해보겠습니다.
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from collections import Counter
# 인위적인 불균형 데이터셋 생성
X, y = make_classification(n_samples=1000, n_features=20, n_informative=4,
n_redundant=3, n_clusters_per_class=2,
weights=[0.90, 0.10], flip_y=0, random_state=42)
plt.figure(figsize=(8, 6))
plt.hist(y, bins=[-0.5, 0.5, 1.5], rwidth=0.6, color='skyblue', edgecolor='black')
plt.xticks([0, 1], ['0', '1'])
plt.title('Imbalanced Data')
plt.xlabel('Class')
plt.ylabel('Frequency')
plt.show()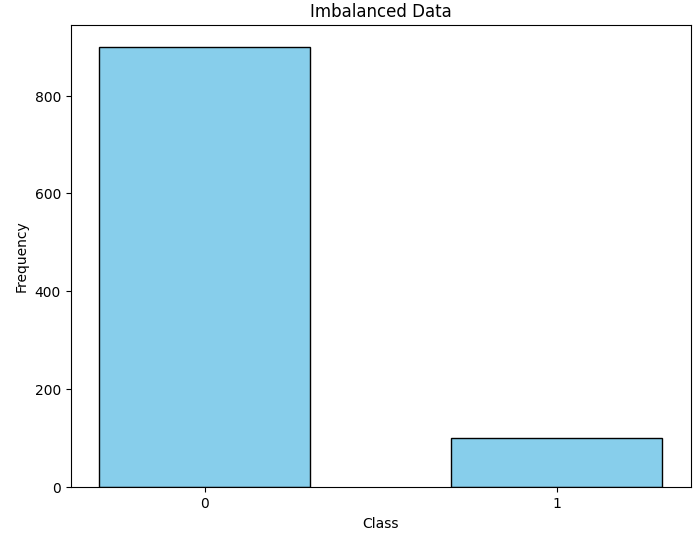
저번 포스팅과 같이 클래스 0이 900개, 클래스 1이 100개인 데이터를 생성하였습니다. 이 데이터를 그대로 이용하여 로지스틱 회귀를 진행한 예측 성능은 아래와 같습니다.
정확도는 좋지만 나머지 성능 지표는 좋지 않죠? 대부분의 데이터를 0으로 분류하는 것을 볼 수 있습니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
logistic = LogisticRegression(random_state = 42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
lo_model = logistic.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
y_pred = lo_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[181 0]
[ 17 2]]
Accuracy: 0.915
Precision: 1.0
Recall (Sensitivity): 0.10526315789473684
F1 Score: 0.1904761904761905
◼️ 오버 샘플링
우선 오버샘플링 먼저 보겠습니다.
오버 샘플링과 언더 샘플링 모두 중요한 점은 원 데이터에 적용하는 것이 아니란 것입니다. 우리가 따로 추출한 train data에 적용을 한 후, 원래 있던 본래의 test 데이터를 통해 성능을 확인해야 합니다!
from imblearn.over_sampling import RandomOverSampler
from collections import Counter
# 랜덤 오버샘플링 수행
ros = RandomOverSampler(random_state=42)
X_res, y_res = ros.fit_resample(X_train, y_train)
count = Counter(y_res)
print(count)
count_raw = Counter(y_train)
print(count_raw)Counter({0: 719, 1: 719})
Counter({0: 719, 1: 81})
이 처럼 원래의 데이터 비율이 719:81 이었지만, 719 : 719로 바뀐것을 볼 수 있습니다. 한번 이렇게 만든 데이터로 똑같은 로지스틱 회귀를 진행해보죠.
logistic = LogisticRegression(random_state = 42)
rov_model = logistic.fit(X_res, y_res)
y_pred_rov = rov_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred_rov)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred_rov)
precision = precision_score(y_test, y_pred_rov)
recall = recall_score(y_test, y_pred_rov)
f1 = f1_score(y_test, y_pred_rov)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[120 61]
[ 9 10]]
Accuracy: 0.65
Precision: 0.14084507042253522
Recall (Sensitivity): 0.5263157894736842
F1 Score: 0.2222222222222222
눈에 띌 정도로 큰 차이는 아니지만 원데이터에 비해 1을 더 잘 분류하는 것을 볼 수 있습니다.(이는 예시이기 때문에 성능이 모두 좋지 않지만, 실제 데이터의 패턴을 사용했을 때는 다를 수 있습니다.)
자살 혹은 질병과 같이 소수 클래스를 잘 분류해내야 하는 생명과 관련된 데이터의 경우를 본다면 비교적 좋은 모델일 수 있다는 가능성이 있네요.
◼️ 언더 샘플링
그렇다면 언더 샘플링은 어떨까요? 언더 샘플링을 이용하여 0과 1을 가진 데이터 모두 개수 81로 맞추어 로지스틱회귀를 진행해봅시다.
from imblearn.under_sampling import RandomUnderSampler
# 랜덤 언더샘플링 수행
rus = RandomUnderSampler(random_state=42)
X_res, y_res = rus.fit_resample(X_train, y_train)
count = Counter(y_res)
print(count)
count_raw = Counter(y_train)
print(count_raw)
logistic = LogisticRegression(random_state = 42)
ruv_model = logistic.fit(X_res, y_res)
y_pred_ruv = ruv_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred_ruv)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred_ruv)
precision = precision_score(y_test, y_pred_ruv)
recall = recall_score(y_test, y_pred_ruv)
f1 = f1_score(y_test, y_pred_ruv)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Counter({0: 81, 1: 81})
Counter({0: 719, 1: 81})
Confusion Matrix:
[[112 69]
[ 8 11]]
Accuracy: 0.615
Precision: 0.1375
Recall (Sensitivity): 0.5789473684210527
F1 Score: 0.22222222222222227
이와 같이 비교적 1에 대해 잘 분류하는 것을 볼 수 있습니다.
파이썬을 통해 살펴보았던 예시는 극단적인 경우이고 임의로 생성한 데이터이기 때문에 랜덤 오버샘플링과 랜덤 언더샘플링의 효과를 확인하기 어려울 수 있습니다. 하지만 앞으로 보게될 SMOTE와 같은 샘플링 기법에 있어서 토대가 되는 내용이기 때문에 알아두면 좋을 것 같습니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| Calibration Plot 과 성능 확인 (0) | 2024.02.27 |
|---|---|
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
저번 포스팅에서 불균형 데이터에 대한 접근법으로 임계값 조정을 확인하였습니다.
불균형 데이터(Imbalanced Data) 접근법 : 임계값(threshold) 조정
불균형 데이터(Imbalaned Data)는 데이터 마이닝 세계에서 생각보다 흔히 마주치는 도전 과제이다. 예를 들면, 자살 예측 혹은 질병 예측과 같은 부분에서 흔하다. 자살 시도 혹은 자살 생각을 하는
datanovice.tistory.com
임계값 조정법은 모델을 적합한 이후에 성능을 확인 한 후 적용하는 방법이었습니다. 이번엔 오버 샘플링과 언더 샘플링입니다.
매우 간단한 방법으로,
오버 샘플링(over sampling)은 소수 클래스의 데이터를 다수 클래스만큼 가상 데이터를 만드는 접근법이며,
언더 샘플링(under sampling)은 다수 클래스의 데이터를 소수 클래스만큼 데이터를 제거하는 접근법입니다.
왜 불균형 데이터를 다루는 것이 중요한지는 위 임계값 조정 포스팅에 다루었으니 한 번씩 확인해주시면 감사하겠습니다!

📌 랜덤 오버샘플링
랜덤 오버샘플링은 소수 클래스의 샘플을 무작위로 복제하여, 소수 클래스의 빈도를 인위적으로 증가시킵니다.
좀 더 수학적으로 본다면 소수 클래스의 확률 분포인(y = 1이 소수라면) P(x|y=1)P(x|y=1)에서 추가 샘플을 추출하는 과정으로 볼 수 있겠죠.
물론 이론적으로 모델이 소수 클래스의 패턴을 더 잘 확인하고 학습할 수 있게 합니다만.. 정해진 분포 안에서 새로운 데이터를 추출하기 때문에 모델이 과적합될 위험이 있습니다.
📌 랜덤 언더샘플링
랜덤 언더샘플링은 다수 클래스의 샘플을 무작위로 제거하여, 클래스 간의 불균형을 줄이는 기법입니다.
이 역시 수학적으로 본다면 다수 클래스 확률 분포 P(x|y=0)P(x|y=0)에서 일부 샘플을 제거하는 과정으로 볼 수 있죠.
이 또한 이론적으로 소수 클래스와 다수 클래스 사이의 경계를 더 명확히 만들어 모델이 학습하기 좋게 만듭니다.
하지만, 언더 샘플링은 다수 클래스의 샘플을 제거하는 만큼 데이터의 정보를 잃는 위험이 있습니다. 주어진 데이터를 잃게 만드는 것은 빅데이터 시대에 큰 단점이라고 볼 수 있습니다. 때문에 언더 샘플링을 사용할 때는 중요한 정보의 손실을 최소화하는 것이 중요할 것입니다.
📌 with python
이번엔 파이썬과 함께 확인해보겠습니다. 이번에도 저번 포스팅과 같이 랜덤한 불균형 데이터를 생성해보겠습니다.
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from collections import Counter
# 인위적인 불균형 데이터셋 생성
X, y = make_classification(n_samples=1000, n_features=20, n_informative=4,
n_redundant=3, n_clusters_per_class=2,
weights=[0.90, 0.10], flip_y=0, random_state=42)
plt.figure(figsize=(8, 6))
plt.hist(y, bins=[-0.5, 0.5, 1.5], rwidth=0.6, color='skyblue', edgecolor='black')
plt.xticks([0, 1], ['0', '1'])
plt.title('Imbalanced Data')
plt.xlabel('Class')
plt.ylabel('Frequency')
plt.show()
저번 포스팅과 같이 클래스 0이 900개, 클래스 1이 100개인 데이터를 생성하였습니다. 이 데이터를 그대로 이용하여 로지스틱 회귀를 진행한 예측 성능은 아래와 같습니다.
정확도는 좋지만 나머지 성능 지표는 좋지 않죠? 대부분의 데이터를 0으로 분류하는 것을 볼 수 있습니다.
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
logistic = LogisticRegression(random_state = 42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
lo_model = logistic.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
y_pred = lo_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[181 0]
[ 17 2]]
Accuracy: 0.915
Precision: 1.0
Recall (Sensitivity): 0.10526315789473684
F1 Score: 0.1904761904761905
◼️ 오버 샘플링
우선 오버샘플링 먼저 보겠습니다.
오버 샘플링과 언더 샘플링 모두 중요한 점은 원 데이터에 적용하는 것이 아니란 것입니다. 우리가 따로 추출한 train data에 적용을 한 후, 원래 있던 본래의 test 데이터를 통해 성능을 확인해야 합니다!
from imblearn.over_sampling import RandomOverSampler
from collections import Counter
# 랜덤 오버샘플링 수행
ros = RandomOverSampler(random_state=42)
X_res, y_res = ros.fit_resample(X_train, y_train)
count = Counter(y_res)
print(count)
count_raw = Counter(y_train)
print(count_raw)Counter({0: 719, 1: 719})
Counter({0: 719, 1: 81})
이 처럼 원래의 데이터 비율이 719:81 이었지만, 719 : 719로 바뀐것을 볼 수 있습니다. 한번 이렇게 만든 데이터로 똑같은 로지스틱 회귀를 진행해보죠.
logistic = LogisticRegression(random_state = 42)
rov_model = logistic.fit(X_res, y_res)
y_pred_rov = rov_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred_rov)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred_rov)
precision = precision_score(y_test, y_pred_rov)
recall = recall_score(y_test, y_pred_rov)
f1 = f1_score(y_test, y_pred_rov)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Confusion Matrix:
[[120 61]
[ 9 10]]
Accuracy: 0.65
Precision: 0.14084507042253522
Recall (Sensitivity): 0.5263157894736842
F1 Score: 0.2222222222222222
눈에 띌 정도로 큰 차이는 아니지만 원데이터에 비해 1을 더 잘 분류하는 것을 볼 수 있습니다.(이는 예시이기 때문에 성능이 모두 좋지 않지만, 실제 데이터의 패턴을 사용했을 때는 다를 수 있습니다.)
자살 혹은 질병과 같이 소수 클래스를 잘 분류해내야 하는 생명과 관련된 데이터의 경우를 본다면 비교적 좋은 모델일 수 있다는 가능성이 있네요.
◼️ 언더 샘플링
그렇다면 언더 샘플링은 어떨까요? 언더 샘플링을 이용하여 0과 1을 가진 데이터 모두 개수 81로 맞추어 로지스틱회귀를 진행해봅시다.
from imblearn.under_sampling import RandomUnderSampler
# 랜덤 언더샘플링 수행
rus = RandomUnderSampler(random_state=42)
X_res, y_res = rus.fit_resample(X_train, y_train)
count = Counter(y_res)
print(count)
count_raw = Counter(y_train)
print(count_raw)
logistic = LogisticRegression(random_state = 42)
ruv_model = logistic.fit(X_res, y_res)
y_pred_ruv = ruv_model.predict(X_test)
# 혼동 행렬
cm = confusion_matrix(y_test, y_pred_ruv)
print("Confusion Matrix:\n", cm)
# 성능 지표 계산
accuracy = accuracy_score(y_test, y_pred_ruv)
precision = precision_score(y_test, y_pred_ruv)
recall = recall_score(y_test, y_pred_ruv)
f1 = f1_score(y_test, y_pred_ruv)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall (Sensitivity): {recall}")
print(f"F1 Score: {f1}")Counter({0: 81, 1: 81})
Counter({0: 719, 1: 81})
Confusion Matrix:
[[112 69]
[ 8 11]]
Accuracy: 0.615
Precision: 0.1375
Recall (Sensitivity): 0.5789473684210527
F1 Score: 0.22222222222222227
이와 같이 비교적 1에 대해 잘 분류하는 것을 볼 수 있습니다.
파이썬을 통해 살펴보았던 예시는 극단적인 경우이고 임의로 생성한 데이터이기 때문에 랜덤 오버샘플링과 랜덤 언더샘플링의 효과를 확인하기 어려울 수 있습니다. 하지만 앞으로 보게될 SMOTE와 같은 샘플링 기법에 있어서 토대가 되는 내용이기 때문에 알아두면 좋을 것 같습니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| Calibration Plot 과 성능 확인 (0) | 2024.02.27 |
|---|---|
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
