수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 조건부 추론 나무(Conditional Inference Trees)
Conditional Inference Trees (CIT)는 통계적 학습의 한 분야에서 비교적 새로운 접근 방식으로, 전통적인 의사결정 나무 모델들이(벌써 의사결정 나무가 전통적인 방법이 되었네요 ㅜ) 직면하는 몇 가지 문제를 해결하고자 하기위해 등장했다.
이 방법론은 의사결정 나무를 구축하는 과정에서 통계적 검정을 사용하여 분할을 결정하는 것이 특징이다. 이러한 접근 방식은 데이터 내의 구조를 탐색할 때 발생할 수 있는 과적합과 변수 선택 편향 문제를 줄이는 데 도움을 준다.
의사결정 나무 생성 알고리즘으로 가장 많이 사용되는 CART 알고리즘은 과적합 방지를 위한 Prunning 그리고 gini index를 이용하는 생성 방법을 가지고 있다. 하지만 변수의 분산에 따른 편향이 있을 수 있다.
Conditional Inference Trees는 Torsten Hothorn, Kurt Hornik, 그리고 Achim Zeileis에 의해 개발되었으며, 2006년에 소개된 이후 주목을 받았으며, 실제 현장에서 사용되는지는 잘 모르겠다.
이 모델은 조건부 모델링 프레임워크를 사용하여 데이터를 분석하고, 각 분할에서 통계적으로 유의미한 차이를 갖는 변수를 선택함으로써 의사결정 나무를 구축한다.
◼️ 핵심 원리
Conditional Inference Trees의 구축 과정은 비교적 단순하다. 먼저, 데이터의 모든 변수에 대해 독립성 검정을 수행하여 타겟 변수와의 관계를 평가한다. 이후, 가장 낮은 p-값을 가진 변수를 선택하여 데이터를 분할합니다. 이러한 과정은 더 이상 통계적으로 유의미한 분할이 없을 때까지, 또는 사용자가 정의한 기준에 도달할 때까지 반복된다.
순열 검정의 일반 이론에 기반해 각 노드에서 가설 검정을 수행하고 나온 p-값을 기반으로 트리를 중단할지 혹은 계속해서 성장 시킬지 결정하는 방법이다.
순열 검정을 이용하여 과정을 설명해보자.
◼️ 순열 검정?
순열 검정(Permutation Test)은 통계적 가설 검정을 수행하는 비모수적(non-parametric) 방법 중 하나이다. 이 방법은 데이터가 특정 가정(예: 정규분포)을 따른다는 전제 없이, 관찰된 데이터의 실제 분포를 이용하여 통계적 유의성을 평가한다.
여기서 말하는 "순열"이란 주어진 데이터 샘플 내에서 가능한 모든 조합을 재배열하는 것을 의미하는데, 순열 검정을 이용한 설명을 단순화해서 조건부 추론 나무에 대해 확인해보자.
◾ 순열 검정의 과정
1. 원래 데이터 샘플 : 우리가 가진 데이터는 두 개 이상의 그룹(예: 처리 그룹과 대조 그룹)으로 나뉘어져 있을 수 있으며, 각 그룹은 다른 결과(y값)을 가질 수 있다.
2. 데이터 섞기 : 순열 검정의 핵심 단계 중 하나는 원래 데이터 샘플에서 y값(결과값)을 무작위로 섞는 것이다. 이는 그룹 간의 차이가 우연히 발생했는지를 확인하기 위함
3. 분할 비교 : 무작위로 섞은 후의 데이터 샘플을 원래의 데이터 샘플과 비교한다. 이 비교는 보통 어떤 통계량(예: 평균 차이)을 사용하여 이루어집니다.
4. p-값 계산 : 이 과정을 여러 번 반복하면, 무작위로 섞은 데이터에서 계산된 통계량의 분포(검정 통계량의 조건부 분포)를 얻을 수 있다.
이 분포를 이용하여, 원래 데이터에서 관찰된 통계량이 얼마나 일반적인지, 혹은 얼마나 특이한지를 평가할 수 있다.
이 때 계산된 p-값은 원래 데이터에서 관찰된 통계량이 무작위로 섞은 데이터에서 얻은 분포와 비교했을 때 얼마나 극단적인지를 나타낸다.
◾ 예시
우리가 식물의 성장에 빛의 색이 미치는 영향을 조사한다고 합시다. 여기서 두 그룹(파란 빛 그룹과 빨간 빛 그룹)이 있고, 각 식물의 성장 높이를 측정하였다.. 우리의 가설은 "빛의 색이 식물의 성장에 유의미한 차이를 만드는가?" 이다.
- 원래 데이터 : 파란 빛 그룹과 빨간 빛 그룹의 식물 성장 높이
- 데이터 섞기 : 식물의 성장 높이(y값)를 무작위로 섞어서 두 그룹에 재할당
- 분할 비교 : 이제 섞인 데이터의 두 그룹 간 성장 높이의 차이를 계산
- p-값 계산 : 이 과정을 많이 반복하여, 원래 데이터에서 관찰된 성장 높이 차이가 무작위로 섞은 데이터에서 얻은 차이의 분포에 비해 얼마나 극단적인지 평가
p-값이 매우 낮다면, 이는 원래 데이터에서 관찰된 결과가 우연히 발생한 것이 아니라는 강력한 증거가 된다. 즉, 빛의 색이 식물의 성장에 유의미한 영향을 미친다고 볼 수 있다.
◾ 그래서 왜 순열 검정을 이용??
다시 트리로 돌아와보자. 우리가 이를 이용하여 각 노드에서 예측 변수에 대한 효과를 순열 검정으로 평가하는 것이 무슨 의미를 가질까?
우선 의사결정 나무에서는 원래 샘플과 무작위 샘플에서의 분할의 효과를 비교한다. 여기서 분할의 효과란 분할이 응답 값의 분포를 얼마나 잘 개선하는지를 측정하는 것이다. (예를 들어, 분할이 응답 값의 분산을 줄이면 분할의 효과는 양수가 된다)
통계적 안정성 확보를 위해 이를 반복한다. 그렇다면 분할의 효과에 대한 분포가 나올 것이고 이에 대한 p-값을 계산한다. 즉, 각 반복에서 생성된 분할의 효과를 사용하여 조건부 분포를 형성하고 이를 통해 원래 샘플에서 얻은 실제 통계량이 얼마나 극단적인지 확인하는 것이다.
중요한 점이 이 조건부 분포라는 점이다. 각 p-값은 특정 조건에 기반하여 생성되었기 때문에, 각 예측 변수에 대한 가설 검정에서 편향되지 않은 결과를 얻을 수 있다.
📌 In R
이를 한번 R에서 확인해보자.
먼저 iris 데이터를 활용한 일반적인 CART 알고리즘이다.
# rpart 패키지를 로드합니다.
library(rpart)
# iris 데이터에 대한 CART 나무를 만듭니다.
model_cart <- rpart(Species ~ ., data = iris)
# 나무를 시각화합니다.
plot(model_cart)
text(model_cart, use.n = TRUE)
install.packages('partykit')
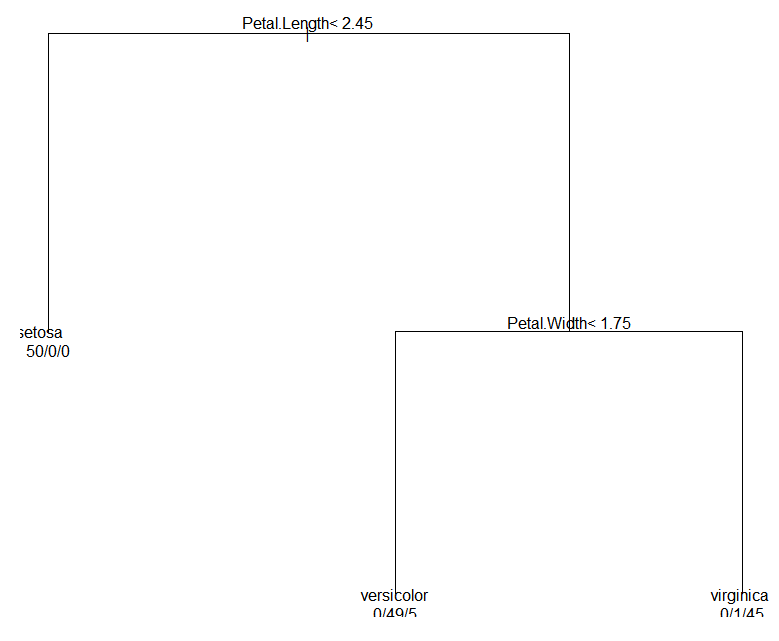
간단한 의사결정 나무로 첫 번째 분리기준은 Petal Lenght < 2.45이고 두 번째 분리 기준은 Petal Width < 1.75이다.
그렇담 이번엔 의사결정 추론 나무를 확인해보자.
# partykit 패키지를 로드합니다. partykit는 party의 후속 패키지입니다.
library(partykit)
# iris 데이터에 대한 조건부 추론 나무를 만듭니다.
model_cit <- ctree(Species ~ ., data = iris)
# 나무를 시각화합니다.
plot(model_cit)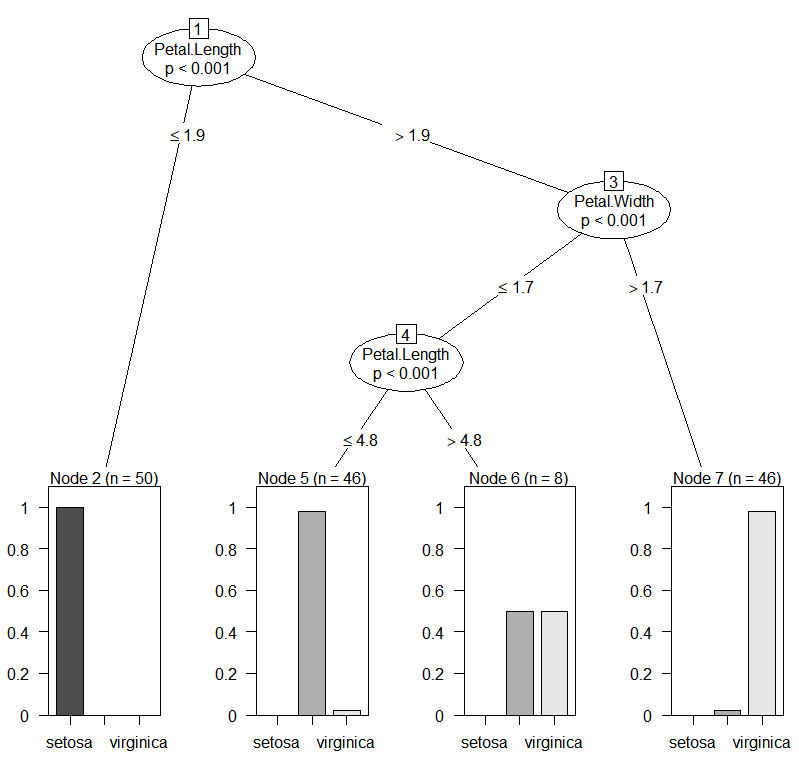
첫 번째와 두 번째 분리기준은 비슷하지만 세 번쨰 분리기준이 생긴 것을 볼 수 있다.(편향되지 않은 선택) 여기서 더욱 중요한 점은 각각의 노드에 적힌 p-값이다. 각각의 p-값이 분리에 있어서 통계적 뒷받침을 해주는 모습니다.
◼️ 장단점
물론 이러한 조건부 추론 나무에도 장단점이 있다.
장점이라 함은 앞서 설명했 듯이 편향되지 않은 변수 선택이 가능하고, 통계적 뒷받침이 존재한다.
단점이라 함은 CART에 비해 트리가 지나치게 커지는 경향이 있어 해석이 어려울 수 있다. 앞서 보았던 iris데이터도 작은 규모이지만 CART에 비해 분리 기준이 더 생긴 것을 볼 수 있다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
|---|---|
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
| 앙상블(Ensemble) : Voting model(Hard, Soft, Weighted) (1) | 2023.12.07 |
📌 조건부 추론 나무(Conditional Inference Trees)
Conditional Inference Trees (CIT)는 통계적 학습의 한 분야에서 비교적 새로운 접근 방식으로, 전통적인 의사결정 나무 모델들이(벌써 의사결정 나무가 전통적인 방법이 되었네요 ㅜ) 직면하는 몇 가지 문제를 해결하고자 하기위해 등장했다.
이 방법론은 의사결정 나무를 구축하는 과정에서 통계적 검정을 사용하여 분할을 결정하는 것이 특징이다. 이러한 접근 방식은 데이터 내의 구조를 탐색할 때 발생할 수 있는 과적합과 변수 선택 편향 문제를 줄이는 데 도움을 준다.
의사결정 나무 생성 알고리즘으로 가장 많이 사용되는 CART 알고리즘은 과적합 방지를 위한 Prunning 그리고 gini index를 이용하는 생성 방법을 가지고 있다. 하지만 변수의 분산에 따른 편향이 있을 수 있다.
Conditional Inference Trees는 Torsten Hothorn, Kurt Hornik, 그리고 Achim Zeileis에 의해 개발되었으며, 2006년에 소개된 이후 주목을 받았으며, 실제 현장에서 사용되는지는 잘 모르겠다.
이 모델은 조건부 모델링 프레임워크를 사용하여 데이터를 분석하고, 각 분할에서 통계적으로 유의미한 차이를 갖는 변수를 선택함으로써 의사결정 나무를 구축한다.
◼️ 핵심 원리
Conditional Inference Trees의 구축 과정은 비교적 단순하다. 먼저, 데이터의 모든 변수에 대해 독립성 검정을 수행하여 타겟 변수와의 관계를 평가한다. 이후, 가장 낮은 p-값을 가진 변수를 선택하여 데이터를 분할합니다. 이러한 과정은 더 이상 통계적으로 유의미한 분할이 없을 때까지, 또는 사용자가 정의한 기준에 도달할 때까지 반복된다.
순열 검정의 일반 이론에 기반해 각 노드에서 가설 검정을 수행하고 나온 p-값을 기반으로 트리를 중단할지 혹은 계속해서 성장 시킬지 결정하는 방법이다.
순열 검정을 이용하여 과정을 설명해보자.
◼️ 순열 검정?
순열 검정(Permutation Test)은 통계적 가설 검정을 수행하는 비모수적(non-parametric) 방법 중 하나이다. 이 방법은 데이터가 특정 가정(예: 정규분포)을 따른다는 전제 없이, 관찰된 데이터의 실제 분포를 이용하여 통계적 유의성을 평가한다.
여기서 말하는 "순열"이란 주어진 데이터 샘플 내에서 가능한 모든 조합을 재배열하는 것을 의미하는데, 순열 검정을 이용한 설명을 단순화해서 조건부 추론 나무에 대해 확인해보자.
◾ 순열 검정의 과정
1. 원래 데이터 샘플 : 우리가 가진 데이터는 두 개 이상의 그룹(예: 처리 그룹과 대조 그룹)으로 나뉘어져 있을 수 있으며, 각 그룹은 다른 결과(y값)을 가질 수 있다.
2. 데이터 섞기 : 순열 검정의 핵심 단계 중 하나는 원래 데이터 샘플에서 y값(결과값)을 무작위로 섞는 것이다. 이는 그룹 간의 차이가 우연히 발생했는지를 확인하기 위함
3. 분할 비교 : 무작위로 섞은 후의 데이터 샘플을 원래의 데이터 샘플과 비교한다. 이 비교는 보통 어떤 통계량(예: 평균 차이)을 사용하여 이루어집니다.
4. p-값 계산 : 이 과정을 여러 번 반복하면, 무작위로 섞은 데이터에서 계산된 통계량의 분포(검정 통계량의 조건부 분포)를 얻을 수 있다.
이 분포를 이용하여, 원래 데이터에서 관찰된 통계량이 얼마나 일반적인지, 혹은 얼마나 특이한지를 평가할 수 있다.
이 때 계산된 p-값은 원래 데이터에서 관찰된 통계량이 무작위로 섞은 데이터에서 얻은 분포와 비교했을 때 얼마나 극단적인지를 나타낸다.
◾ 예시
우리가 식물의 성장에 빛의 색이 미치는 영향을 조사한다고 합시다. 여기서 두 그룹(파란 빛 그룹과 빨간 빛 그룹)이 있고, 각 식물의 성장 높이를 측정하였다.. 우리의 가설은 "빛의 색이 식물의 성장에 유의미한 차이를 만드는가?" 이다.
- 원래 데이터 : 파란 빛 그룹과 빨간 빛 그룹의 식물 성장 높이
- 데이터 섞기 : 식물의 성장 높이(y값)를 무작위로 섞어서 두 그룹에 재할당
- 분할 비교 : 이제 섞인 데이터의 두 그룹 간 성장 높이의 차이를 계산
- p-값 계산 : 이 과정을 많이 반복하여, 원래 데이터에서 관찰된 성장 높이 차이가 무작위로 섞은 데이터에서 얻은 차이의 분포에 비해 얼마나 극단적인지 평가
p-값이 매우 낮다면, 이는 원래 데이터에서 관찰된 결과가 우연히 발생한 것이 아니라는 강력한 증거가 된다. 즉, 빛의 색이 식물의 성장에 유의미한 영향을 미친다고 볼 수 있다.
◾ 그래서 왜 순열 검정을 이용??
다시 트리로 돌아와보자. 우리가 이를 이용하여 각 노드에서 예측 변수에 대한 효과를 순열 검정으로 평가하는 것이 무슨 의미를 가질까?
우선 의사결정 나무에서는 원래 샘플과 무작위 샘플에서의 분할의 효과를 비교한다. 여기서 분할의 효과란 분할이 응답 값의 분포를 얼마나 잘 개선하는지를 측정하는 것이다. (예를 들어, 분할이 응답 값의 분산을 줄이면 분할의 효과는 양수가 된다)
통계적 안정성 확보를 위해 이를 반복한다. 그렇다면 분할의 효과에 대한 분포가 나올 것이고 이에 대한 p-값을 계산한다. 즉, 각 반복에서 생성된 분할의 효과를 사용하여 조건부 분포를 형성하고 이를 통해 원래 샘플에서 얻은 실제 통계량이 얼마나 극단적인지 확인하는 것이다.
중요한 점이 이 조건부 분포라는 점이다. 각 p-값은 특정 조건에 기반하여 생성되었기 때문에, 각 예측 변수에 대한 가설 검정에서 편향되지 않은 결과를 얻을 수 있다.
📌 In R
이를 한번 R에서 확인해보자.
먼저 iris 데이터를 활용한 일반적인 CART 알고리즘이다.
# rpart 패키지를 로드합니다.
library(rpart)
# iris 데이터에 대한 CART 나무를 만듭니다.
model_cart <- rpart(Species ~ ., data = iris)
# 나무를 시각화합니다.
plot(model_cart)
text(model_cart, use.n = TRUE)
install.packages('partykit')

간단한 의사결정 나무로 첫 번째 분리기준은 Petal Lenght < 2.45이고 두 번째 분리 기준은 Petal Width < 1.75이다.
그렇담 이번엔 의사결정 추론 나무를 확인해보자.
# partykit 패키지를 로드합니다. partykit는 party의 후속 패키지입니다.
library(partykit)
# iris 데이터에 대한 조건부 추론 나무를 만듭니다.
model_cit <- ctree(Species ~ ., data = iris)
# 나무를 시각화합니다.
plot(model_cit)
첫 번째와 두 번째 분리기준은 비슷하지만 세 번쨰 분리기준이 생긴 것을 볼 수 있다.(편향되지 않은 선택) 여기서 더욱 중요한 점은 각각의 노드에 적힌 p-값이다. 각각의 p-값이 분리에 있어서 통계적 뒷받침을 해주는 모습니다.
◼️ 장단점
물론 이러한 조건부 추론 나무에도 장단점이 있다.
장점이라 함은 앞서 설명했 듯이 편향되지 않은 변수 선택이 가능하고, 통계적 뒷받침이 존재한다.
단점이라 함은 CART에 비해 트리가 지나치게 커지는 경향이 있어 해석이 어려울 수 있다. 앞서 보았던 iris데이터도 작은 규모이지만 CART에 비해 분리 기준이 더 생긴 것을 볼 수 있다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
|---|---|
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
| 앙상블(Ensemble) : Voting model(Hard, Soft, Weighted) (1) | 2023.12.07 |
