수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 Ensemble : Voting model
오늘은 앙상블 모델 중 voting model에 대해 알아볼까 합니다. 전에 포스팅했던 Bagging의 경우도 투표를 하지만, Voting model의 경우 여러 모델을 학습하여 각 모델의 결과를 이용하여 투표하는 것이고, Bagging의 경우 하나의 모델에서 여러 데이터셋의 split을 이용한 방법입니다.
◼️ 분류에서(Hard Voting, Soft Voting)
우선 $m$개의 분류모델 $\hat{f}_1, ..., \hat{f}_m$이 있을 때 예측값을 $\hat{Y}_j(\textbf{x}) = \hat{f}_j$라고 합시다.
투표 방법에는 Hard Voting, Soft Voting이 있습니다.
1️⃣ Hard Voting
Hard Voting에서는 말그대로 '다수결'을 이용합니다. 만약 과반수의 모델이 $\hat{Y}(\textbf{x}) = A$라고 예측했다면 전체 예측값을 $A$라고 반환합니다.
$$
\hat{Y}(\textbf{x}) = \text{majority vote of } [\hat{Y}_1(\textbf{x}),..., \hat{Y}_m(\textbf{x})]
$$
2️⃣ Soft Voting
Soft Voting에서는 사후 확률 추정치의 평균을 계산하고 평균을 최대화하여 관측치의 클래스를 예측합니다.
쉽게 설명하면 각 모델이 어떤 클래스일지에 대한 확률을 고려하고, 이 예측의 확률을 평균 냅니다. 그 평균에서 가장 높은 확률을 갖는 클래스를 최종적인 예측 클래스로 선택하는 것입니다.
가장 가능성이 높은 클래스를 골라 전체 분류기의 평균적인 의견을 따르는 것입니다.
$$
\hat{Y}(\textbf{x}) = \arg\max_k \dfrac1m \sum^m_{j=1} \hat{p}_{jk}(\textbf{x})
$$
$\hat{p}_{jk}(\textbf{x})$는 $\hat{P}(Y=k|\textbf{x}, M_j)$이고(사후 확률) $M_j$는 $j$번째 모델입니다.
아래 코드는 임의의 데이터를 생성하고 로지스틱 회귀, 서포트 벡터 머신, 결정 트리라는 3개의 모델을 사용하여 Voting 하는 코드입니다. Hard Voting과 Soft Voting입니다.
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import accuracy_score
# 데이터 생성
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2,
n_classes=3, n_redundant=0, n_clusters_per_class=1)
# 분류기 생성
clf1 = LogisticRegression(random_state=42)
clf2 = SVC(probability=True, random_state=42)
clf3 = DecisionTreeClassifier(random_state=42)
# 각 분류기 별 결정 경계 시각화 함수
def plot_decision_boundary(clf, X, y, title):
h = .02 # step size in the mesh
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, marker='o', edgecolors='k')
plt.title(title)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
# 하드 보팅
hard_voting_clf = VotingClassifier(estimators=[('lr', clf1), ('svm', clf2), ('dt', clf3)], voting='hard')
hard_voting_clf.fit(X, y) # model fitting
## 하드 보팅 정확도 확인(not test set)
hard_voting_pred = hard_voting_clf.predict(X)
hard_voting_accuracy = accuracy_score(y, hard_voting_pred)
print(f'Hard Voting Accuracy: {hard_voting_accuracy}')
plot_decision_boundary(hard_voting_clf, X, y, 'Hard Voting Decision Boundary')
# 소프트 보팅
soft_voting_clf = VotingClassifier(estimators=[('lr', clf1), ('svm', clf2), ('dt', clf3)], voting='soft')
soft_voting_clf.fit(X, y) # model fitting
## 소프트 보팅 정확도 확
soft_voting_pred = soft_voting_clf.predict(X)
soft_voting_accuracy = accuracy_score(y, soft_voting_pred)
print(f'Soft Voting Accuracy: {soft_voting_accuracy}')
plot_decision_boundary(soft_voting_clf, X, y, 'Soft Voting Decision Boundary')
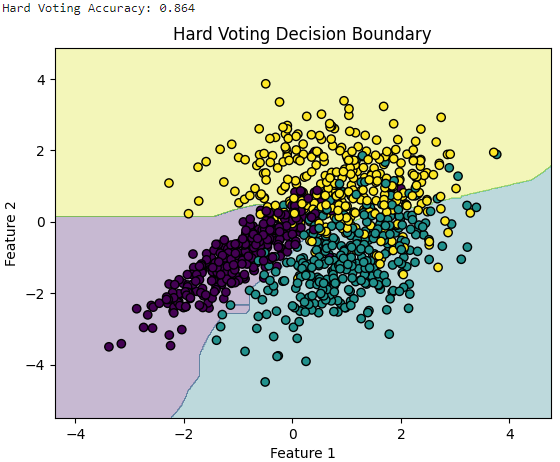

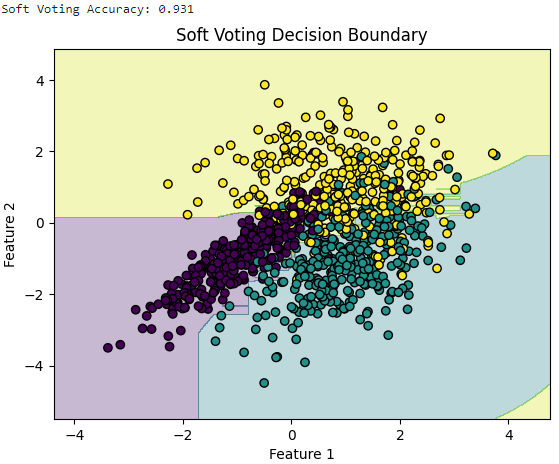
◼️ 회귀에서(With Weighted Voting)
회귀의 경우 모든 모델에서 예측한 값의 평균을 내어 최종 예측값으로 반환합니다.
$$
\hat{f}(\textbf{x}) = \dfrac1m \hat{f}_j(\textbf{x})
$$
아래 코드는 회귀에서의 voting입니다.
rom sklearn.ensemble import VotingRegressor
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import make_regression
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import numpy as np
# 회귀용 데이터 생성
X, y = make_regression(n_samples=1000, n_features=1, noise=10)
# 회귀 모델 생성
reg1 = LinearRegression()
reg2 = SVR()
reg3 = DecisionTreeRegressor()
# Voting regression
voting_reg = VotingRegressor(estimators=[('lr', reg1), ('svr', reg2), ('dt', reg3)], n_jobs=-1)
voting_reg.fit(X, y)
voting_pred = voting_reg.predict(X)
voting_mse = mean_squared_error(y, voting_pred)
print(f'Voting MSE: {voting_mse}')
Voting MSE: 211.9694759532453
3️⃣ Weighted Voting
위에선 X, y를 train, test로 분류하지 않고 간단하게 알아봤습니다. 하지만 실제로 성능을 측정하기 위해선 train, test로 나누어 독립적인 세트에서 성능을 확인해야 합니다.
이를 통해 이용할 수 있는 voting 방법 중 하나가 Weighted Voting입니다. 검증 세트에서 어떠한 성능 측정 지표를 이용하여 가중치로 사용합니다. 정확도(Accuracy)도 될 수 있고, AUC(Area Under the Curve)가 될 수도 있습니다. 회귀의 경우 RMSE, MSE가 될수도 있죠.
이들을 순위 매겨 잘 예측한 모델들의 가중치를 늘리고 반대로 예측하지 못한 모델들의 가중치는 낮은 값으로 설정하여 Voting을 하는 것입니다.
아래 코드는 X, y를 train, test, validiation set로 나누어 train으로 각 모델을 학습시킨 후, validation set을 이용하여 MSE를 계산하고 가중치를 계산합니다.
그 후 각 가중치를 이용하여 Weighted voting을 train set에 대해 학습한 후, 최종적으로 test set으로 성능을 확인하는 코드입니다.
from sklearn.ensemble import VotingRegressor
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# 회귀용 데이터 생성
X, y = make_regression(n_samples=1000, n_features=2, noise=20, random_state=42)
# 데이터를 train, validation, test set으로 나누기
X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.3, random_state=42)
X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)
# 회귀 모델 생성
reg1 = LinearRegression()
reg2 = SVR()
# 모델 학습
reg1.fit(X_train, y_train)
reg2.fit(X_train, y_train)
# 각 모델의 성능 측정
reg1_val_pred = reg1.predict(X_val)
reg2_val_pred = reg2.predict(X_val)
mse_reg1 = mean_squared_error(y_val, reg1_val_pred)
mse_reg2 = mean_squared_error(y_val, reg2_val_pred)
print(f'선형 회귀 MSE : {mse_reg1}')
print(f'서포트 벡터 머신 MSE : {mse_reg2}')
# 가중치 계산
weight_reg1 = 1 / (1 + mse_reg1)
weight_reg2 = 1 / (1 + mse_reg2)
print(f'선형 회귀 가중치 : {weight_reg1}, 서포트 벡터 머신 가중치 : {weight_reg2}')
# 가중 Voting Regression
weighted_voting_reg = VotingRegressor(estimators=[('lr', reg1), ('svr', reg2)], weights=[weight_reg1, weight_reg2])
weighted_voting_reg.fit(X_train, y_train)
# Test set에서의 성능 평가
weighted_voting_pred = weighted_voting_reg.predict(X_test)
weighted_voting_mse = mean_squared_error(y_test, weighted_voting_pred)
weighted_voting_r2 = r2_score(y_test, weighted_voting_pred)
print(f'Weighted Voting Regression MSE: {weighted_voting_mse}')
print(f'Weighted Voting Regression R2 Score: {weighted_voting_r2}')선형 회귀 MSE : 422.36928492360045
서포트 벡터 머신 MSE : 813.8995274777825
선형 회귀 가중치 : 0.0023620041311699217,
서포트 벡터 머신 가중치 : 0.001227145146463794
Weighted Voting Regression MSE: 353.1277500137568
Weighted Voting Regression R2 Score: 0.7829944100165228
결과를 보면 train set에서 선형회귀의 MSE가 더 작아 가중치를 더 주었고, 최종 voting model의 예측의 R^2는 0.78로 준수한 성능을 보였습니다.
'🌞 Statistics for AI > Machine learning' 카테고리의 다른 글
| 의사결정 나무(Decision tree) 알고리즘 : ID3, CART (0) | 2024.02.19 |
|---|---|
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
| ROC, AUC (ROC curve 그리는 법) (0) | 2023.12.05 |
| Cohen's kappa(코헨의 카파) (1) | 2023.12.05 |
| 혼동 행렬(Confusion Matrix) 설명 (1) | 2023.12.05 |
