수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 의사결정 나무와 알고리즘들
의사결정 나무(Decision Tree)는 데이터 과학의 강력한 도구로, 복잡한 데이터 세트로부터 의미 있는 정보를 추출하고 예측 모델을 구축하는 데 널리 사용된다.
실제로 우리 Data mining, ML에 관해 공부할 때 거의 기초 수준으로 공부하고 볼 수 있는 모델이다.
이 방법론은 그 이름에서 알 수 있듯이, 결정 규칙을 나무 구조로 조직화하여 결과를 도출한다. 각 분기는 데이터의 특성에 따른 결정 과정을 나타내며, 최종적으로 리프 노드에 도달하여 결론을 내린다. 이러한 과정은 복잡한 의사 결정 과정을 직관적이고 이해하기 쉬운 방식으로 시각화할 수 있게 해준다.(가장 큰 장점)
의사결정 나무의 핵심 가치는 그 간결함에 있다. 데이터의 내재된 패턴을 명확하게 파악할 수 있을 뿐만 아니라, 모델의 예측이 어떻게 이루어지는지도 손쉽게 이해할 수 있다는 점. 이는 몇몇 다른 많은 머신러닝 기법들이(특히 블랙박스 모델) 제공하지 못하는 투명성과 해석 가능성을 의사결정 나무에게 부여한다.
이 블로그 포스트에서는 의사결정 나무의 기본 원리를 소개하고, 특히 두 가지 중요한 알고리즘인 ID3(Iterative Dichotomiser 3)와 CART(Classification and Regression Trees)에 대해 깊이 있게 다룰 예정이다. 이 알고리즘들은 의사결정 나무를 구축하는 과정에서 중요한 역할을 하며, 각각 고유한 접근 방식과 장단점을 가지고 있다.(보통은 CART를 주로 사용하는 듯하다.)
ID3 알고리즘은 정보 이득(Information Gain)을 기반으로 가장 유용한 속성을 선택하여 트리를 분할하는 전략을 사용한다. 이 방법은 주로 분류 문제에 적합하며, 데이터에서 가장 정보력이 높은 속성을 찾아 의사결정 과정을 진행한다.
반면, CART 알고리즘은 분류 뿐만 아니라 회귀 문제에도 적용될 수 있는 유연성을 제공한다. 이 알고리즘은 지니 불순도(Gini Impurity) 또는 평균 제곱 오차(Mean Squared Error)와 같은 기준을 사용하여 데이터를 가장 효과적으로 분할할 수 있는 지점을 찾는다.
이러한 알고리즘들을 통해 우리는 데이터 내의 복잡한 관계와 패턴을 이해하고, 예측 모델을 구축하는 데 있어 중요한 인사이트를 얻을 수 있다.
📌 의사 결정 나무
앞서 설명한 것과 같이 의사결정 나무는 특정 분리기준에 의하여 가지로 나뉘고 최종 리프노드에 결론이 있는 나무의 역구조로 이루어져 있다.
예를 들어, 우리에게 익숙한 iris 데이터를 이용하여 한번 확인해보자.
# 필요한 라이브러리를 불러옵니다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
# 데이터 불러오기
iris = load_iris()
X, y = iris.data, iris.target
# 의사결정 나무 모델 생성 및 학습
dt_clf = DecisionTreeClassifier()
dt_clf.fit(X, y)
# 모델의 결정 트리 시각화
plt.figure(figsize=(20,10))
plot_tree(dt_clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names, rounded=True)
plt.show()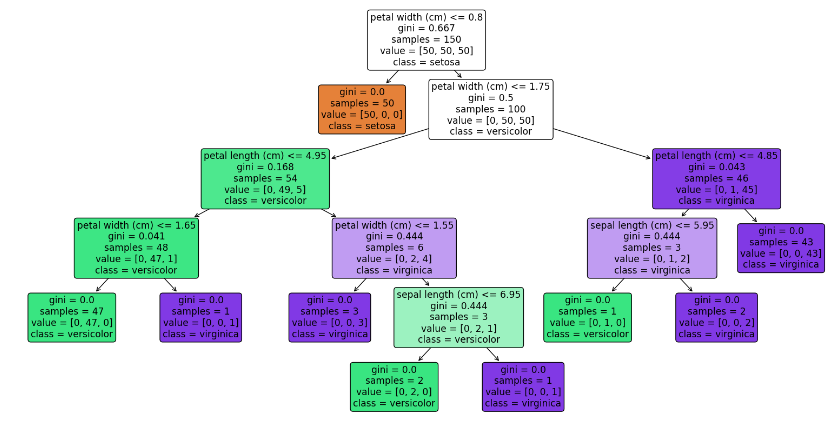
이와 같이 맨 처음 하나의 노드로 시작하여 뻗어 나가며 각각의 분기의 결정 규칙에 따라 여러 가지로 나뉜다. 더이상 나눠지지 않는 가지에는 각각의 클래스가 적혀있다.
가운데 맨 아래 노드를 보면 sepal length가 6.95와 같거나 작은가 혹은 큰가를 기준으로 나뉘어져 있고 이를 통해 왼쪽아래 노드에는 versicolor, 오른쪽 아래 노드에는 virginica로 분류된다.
굳이 이렇게 보여주지 않아도, 의사결정 나무는 한눈에 보았을 때 이해하기 쉽다. 굳이 전문가가 아니라도 말이다.
그렇담 중요한 것은 과연 어떻게 이 의사결정 나무를 구성하는가? 이다.
◼️ ID3(Iterative DIchotomiser 3) 알고리즘
ID3(Iterative Dichotomiser 3) 알고리즘은 의사결정 나무를 구축하는 고전적인 방법 중 하나로, 정보 이득(Information Gain) 개념을 기반으로 한다. 이 알고리즘은 Ross Quinlan에 의해 1980년대 초반에 개발되었으며, 주로 분류 문제에 사용된다.
ID3는 데이터 세트의 각 속성에 대한 정보 이득을 계산하고, 가장 높은 정보 이득을 가진 속성을 사용하여 데이터 세트를 분할합니다. 이 과정은 모든 데이터가 동일한 클래스에 속하거나, 더 이상 분할할 속성이 없을 때까지 재귀적으로 반복됩니다.
구체적으로?? 윈도우(window)라고 불리는 훈련 세트의 하위 집합을 임의로 선택하고 이를 기반으로 의사결정 트리를 생성한다. 해당 트리는 윈도우 안의 모든 객체를 올바르게 분류해내고, 이렇게 만든 트리로 윈도우에 포함되지 않은 객체를 분류한다.
만약 모두 올바르게 분류한다면? 과정은 끝이난다. 문제는 올바르게 분류하지 못한다면?이다. 이게 중요한 점인데, 오분류된 객체들을 윈도우에 추가한 후, 다시 의사결정 트리를 생성하고 앞선 과정이 반복된다.
해당 과정은 실제 모든 훈련 세트를 사용하는 것 보다는 빠르다고 한다. 하지만 O'Keefe(1983)은 해당 과정이 모든 훈련 세트를 포함할 수 있을 때까지 수렴하지 못할 수도 있다고 지적하였다.
◾ 정보 이득(Information Gain)
정보 이득은 특정 속성을 사용하여 데이터 세트를 분할했을 때 얻을 수 있는 정보량의 증가를 나타낸다. 정보 이득은 엔트로피(Entropy)라는 개념을 사용하여 계산된다.
엔트로피는 데이터 세트의 불확실성 또는 무질서도를 측정하는데 사용되며, 정보 이득은 분할 전후의 엔트로피 차이로 정의됩니다.
◾ 엔트로피(Entropy)
데이터 세트 $S$의 엔트로피는 다음과 같이 계산된다.(많이 보았을 것이다)
$H(S) = - \sum_{i=1}^{n} p_i \log_2 p_i$
여기서, $p_i$는 데이터 세트 $S$ 내에서 클래스 $i$의 비율을 나타낸다.
◾ 정보 이득 계산
feature $A$에 대한 정보 이득은 다음과 같이 계산된다.
$IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)$
여기서, $IG(S, A)$는 fature $A$를 사용하여 데이터 세트 $S$를 분할했을 때의 정보 이득.
$H(S)$는 원래 세트의 엔트로피, $Values(A)$는 속성 $A$가 취할 수 있는 모든 값들의 집합.
$|S_v|$는 속성 $A$의 값이 $v$일 때의 세트 크기, $H(S_v)$는 속성 $A$의 값이 $v$일 때의 세트의 엔트로피를 나타낸다.
ID3 알고리즘은 이 정보 이득을 최대화하는 속성을 찾아 해당 속성으로 데이터 세트를 분할한다.
이러한 방법을 feature A뿐 아닌 모든 feature에 대해 반복 계산하고 $IG$(information gain)을 최대화 하는 feature를 선택하여 분할한 후, 다음 단계에서 다른 feature들로 반복해나가는 것이다.
앞서 보았던 파이썬 예시는 gini 계수로 CART 알고리즘을 활용한 것이다. 파이썬에서 완벽한 ID3 알고리즘을 구현하지는 않아도 분류기준을 entropy로 바꾸어 구현해볼 수 있다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
# 데이터 불러오기
iris = load_iris()
X, y = iris.data, iris.target
# 의사결정 나무 모델 생성 (ID3 비슷한 방식으로)
# 'entropy' 기준을 사용해 엔트로피를 기반으로 하는 의사결정 나무 생성
dt_clf = DecisionTreeClassifier(criterion='entropy')
dt_clf.fit(X, y)
# 모델의 결정 트리 시각화
plt.figure(figsize=(20,10))
plot_tree(dt_clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names, rounded=True)
plt.show()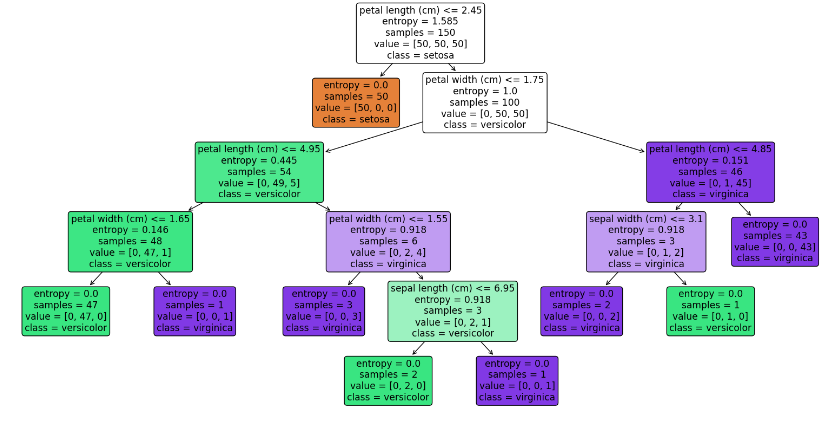
확인해 보면 앞서 보았던 그림과 다르게 gini가 아닌 entropy가 사용된 것을 볼 수 있다!
◾ 장단점
ID3 알고리즘의 장점은 매우 직관적으로 생각보다 패턴을 잘 식별한다는 점이다.(특히 범주형에서) 또한 계산 비용이 적다.
단점이라함은, 과적합의 위험이 크고 연속형 변수처리가 어렵다. 또한 불균형 데이터와 결측치 데이터에 민감하고 처리하기 어렵다.
◼️ CART(Calssification and Regression Trees) 알고리즘
CART의 경우 앞선 포스팅에서 다룬 적이 있었다. ID3 알고리즘과의 차이와 구별점을 보기위해 다시한번 알아보자.
CART(Classification and Regression Trees) 알고리즘은 분류 및 회귀 문제에 사용될 수 있는 결정 트리 모델을 구축하기 위한 방법론이다.
1984년 Leo Breiman, Jerome Friedman, Richard Olshen, 그리고 Charles Stone에 의해 소개된 이 알고리즘은 데이터를 두 개의 하위 그룹으로 반복적으로 분할하여 트리를 구성한다.(찾아보니 논문이 아닌 서적이여서 찾기가 힘드네요 ㅜㅜ)
CART는 분류 문제(Classification)와 연속적 값을 예측하는 회귀 문제(Regression) 모두에 적용될 수 있는 범용적인 모델이다.
여기서 알 수 있는 ID3와의 차이점은 2가지로 첫 번째는 ID3와 다르게 CART는 하나의 노드에 대한 하위노드가 2개입이다. 즉, 분할은 꼭 양갈래로만 이루어 진다는 점. 그리고 두 번째는 ID3와 다르게 회귀 문제에서도 적용가능 하다는 점이다.
◾ CART의 핵심 원리
CART 알고리즘은 특정 속성에 대한 최적의 분할을 찾기 위해 불순도(impurity) 또는 오차(error) 기준을 사용하는데, 이러한 기준은 문제의 유형(분류 또는 회귀)에 따라 달라진다.
분류 문제의 경우, CART는 주로 지니 불순도(Gini Impurity)를 사용한다.(엔트로피(Entropy)를 사용할 수도 있다)
지니 불순도의 계산을 아래와 같다.
$Gini(S) = 1 - \sum_{i=1}^{n} p_i^2$
여기서, $p_i$는 ID3에서 본 것과 같이 특정 클래스에 속하는 데이터 포인트의 비율을 나타냅니다.
회귀 문제의 경우, CART는 데이터 포인트와 분할 후 각 그룹의 평균 간의 평균 제곱 오차(Mean Squared Error, MSE) 또는 평균 절대 오차(Mean Absolute Error, MAE)를 최소화하는 방식으로 분할을 결정합니다.
◾ 분할 과정
1. 최적의 분할 찾기: CART는 각 단계에서 모든 가능한 분할을 평가하고, 가장 높은 불순도 감소(분류) 또는 오차 감소(회귀)를 제공하는 분할을 선택한다.(ID3와 같이 모든 feature와 모든 분리기준을 사용)
2. 재귀적 분할 : 선택된 최적의 분할을 사용하여 데이터를 두 하위 그룹으로 분할한 다음, 이 과정을 각 하위 그룹에 대해 반복적으로 수행한다. 이 과정은 더 이상 분할이 불가능하거나 사용자가 설정한 트리의 최대 깊이에 도달할 때까지 계속된다.(ID3와 같이 이를 반복한다)
3. 가지치기(Pruning) : 과적합을 방지하기 위해, CART는 생성된 트리를 가지치기하는 과정을 포함한다. 이는 복잡한 트리에서 일부 노드를 제거하여 더 간단한 모델을 만드는 과정을 의미한다.
해당 가지치기가 ID3와 비교되는 차이점이다. ID3와 다르게 CART에서는 과적합 방지를 위해 너무나 광범위하고 세부적인 나무의 가지를 잘라서 간결하고 일바화 가능성이 높은 나무를 생성하는 것입니다.
이에 대한 내용은 이미 포스팅 한 적이 있으니 한번 확인해보시면 좋을 것 같습니다. (링크 : 프루닝)
📌 정리
ID3 그리고 CART에 대해 알아보았습니다. 이 전에 ID3의 한계점을 조금이나마 극복하기 위해 개발된 C4.5 알고리즘도 있으나, 본 포스팅에서 다루진 않았습니다. ID3와 비슷한 방법으로 찾아보면 이해하기 쉬울 것입니다!
현직이 아닌 공부하는 사람으로서 자세히 알지는 모르지만 대부분의 트리 구조 모델에서 CART 알고리즘을 사용하는 것 같더군요. 앞서 포스팅에서도 보았지만 ID3에 비해 과적합면에서도 상위 버전이고 회귀에서도 적용된다는 점이 클 것 같습니다. 또한 CART 알고리즘은 타 알고리즘과 다르게 통계학 분야에서 만들어졌다고 합니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
|---|---|
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
| 앙상블(Ensemble) : Voting model(Hard, Soft, Weighted) (1) | 2023.12.07 |
| ROC, AUC (ROC curve 그리는 법) (2) | 2023.12.05 |
📌 의사결정 나무와 알고리즘들
의사결정 나무(Decision Tree)는 데이터 과학의 강력한 도구로, 복잡한 데이터 세트로부터 의미 있는 정보를 추출하고 예측 모델을 구축하는 데 널리 사용된다.
실제로 우리 Data mining, ML에 관해 공부할 때 거의 기초 수준으로 공부하고 볼 수 있는 모델이다.
이 방법론은 그 이름에서 알 수 있듯이, 결정 규칙을 나무 구조로 조직화하여 결과를 도출한다. 각 분기는 데이터의 특성에 따른 결정 과정을 나타내며, 최종적으로 리프 노드에 도달하여 결론을 내린다. 이러한 과정은 복잡한 의사 결정 과정을 직관적이고 이해하기 쉬운 방식으로 시각화할 수 있게 해준다.(가장 큰 장점)
의사결정 나무의 핵심 가치는 그 간결함에 있다. 데이터의 내재된 패턴을 명확하게 파악할 수 있을 뿐만 아니라, 모델의 예측이 어떻게 이루어지는지도 손쉽게 이해할 수 있다는 점. 이는 몇몇 다른 많은 머신러닝 기법들이(특히 블랙박스 모델) 제공하지 못하는 투명성과 해석 가능성을 의사결정 나무에게 부여한다.
이 블로그 포스트에서는 의사결정 나무의 기본 원리를 소개하고, 특히 두 가지 중요한 알고리즘인 ID3(Iterative Dichotomiser 3)와 CART(Classification and Regression Trees)에 대해 깊이 있게 다룰 예정이다. 이 알고리즘들은 의사결정 나무를 구축하는 과정에서 중요한 역할을 하며, 각각 고유한 접근 방식과 장단점을 가지고 있다.(보통은 CART를 주로 사용하는 듯하다.)
ID3 알고리즘은 정보 이득(Information Gain)을 기반으로 가장 유용한 속성을 선택하여 트리를 분할하는 전략을 사용한다. 이 방법은 주로 분류 문제에 적합하며, 데이터에서 가장 정보력이 높은 속성을 찾아 의사결정 과정을 진행한다.
반면, CART 알고리즘은 분류 뿐만 아니라 회귀 문제에도 적용될 수 있는 유연성을 제공한다. 이 알고리즘은 지니 불순도(Gini Impurity) 또는 평균 제곱 오차(Mean Squared Error)와 같은 기준을 사용하여 데이터를 가장 효과적으로 분할할 수 있는 지점을 찾는다.
이러한 알고리즘들을 통해 우리는 데이터 내의 복잡한 관계와 패턴을 이해하고, 예측 모델을 구축하는 데 있어 중요한 인사이트를 얻을 수 있다.
📌 의사 결정 나무
앞서 설명한 것과 같이 의사결정 나무는 특정 분리기준에 의하여 가지로 나뉘고 최종 리프노드에 결론이 있는 나무의 역구조로 이루어져 있다.
예를 들어, 우리에게 익숙한 iris 데이터를 이용하여 한번 확인해보자.
# 필요한 라이브러리를 불러옵니다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
# 데이터 불러오기
iris = load_iris()
X, y = iris.data, iris.target
# 의사결정 나무 모델 생성 및 학습
dt_clf = DecisionTreeClassifier()
dt_clf.fit(X, y)
# 모델의 결정 트리 시각화
plt.figure(figsize=(20,10))
plot_tree(dt_clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names, rounded=True)
plt.show()
이와 같이 맨 처음 하나의 노드로 시작하여 뻗어 나가며 각각의 분기의 결정 규칙에 따라 여러 가지로 나뉜다. 더이상 나눠지지 않는 가지에는 각각의 클래스가 적혀있다.
가운데 맨 아래 노드를 보면 sepal length가 6.95와 같거나 작은가 혹은 큰가를 기준으로 나뉘어져 있고 이를 통해 왼쪽아래 노드에는 versicolor, 오른쪽 아래 노드에는 virginica로 분류된다.
굳이 이렇게 보여주지 않아도, 의사결정 나무는 한눈에 보았을 때 이해하기 쉽다. 굳이 전문가가 아니라도 말이다.
그렇담 중요한 것은 과연 어떻게 이 의사결정 나무를 구성하는가? 이다.
◼️ ID3(Iterative DIchotomiser 3) 알고리즘
ID3(Iterative Dichotomiser 3) 알고리즘은 의사결정 나무를 구축하는 고전적인 방법 중 하나로, 정보 이득(Information Gain) 개념을 기반으로 한다. 이 알고리즘은 Ross Quinlan에 의해 1980년대 초반에 개발되었으며, 주로 분류 문제에 사용된다.
ID3는 데이터 세트의 각 속성에 대한 정보 이득을 계산하고, 가장 높은 정보 이득을 가진 속성을 사용하여 데이터 세트를 분할합니다. 이 과정은 모든 데이터가 동일한 클래스에 속하거나, 더 이상 분할할 속성이 없을 때까지 재귀적으로 반복됩니다.
구체적으로?? 윈도우(window)라고 불리는 훈련 세트의 하위 집합을 임의로 선택하고 이를 기반으로 의사결정 트리를 생성한다. 해당 트리는 윈도우 안의 모든 객체를 올바르게 분류해내고, 이렇게 만든 트리로 윈도우에 포함되지 않은 객체를 분류한다.
만약 모두 올바르게 분류한다면? 과정은 끝이난다. 문제는 올바르게 분류하지 못한다면?이다. 이게 중요한 점인데, 오분류된 객체들을 윈도우에 추가한 후, 다시 의사결정 트리를 생성하고 앞선 과정이 반복된다.
해당 과정은 실제 모든 훈련 세트를 사용하는 것 보다는 빠르다고 한다. 하지만 O'Keefe(1983)은 해당 과정이 모든 훈련 세트를 포함할 수 있을 때까지 수렴하지 못할 수도 있다고 지적하였다.
◾ 정보 이득(Information Gain)
정보 이득은 특정 속성을 사용하여 데이터 세트를 분할했을 때 얻을 수 있는 정보량의 증가를 나타낸다. 정보 이득은 엔트로피(Entropy)라는 개념을 사용하여 계산된다.
엔트로피는 데이터 세트의 불확실성 또는 무질서도를 측정하는데 사용되며, 정보 이득은 분할 전후의 엔트로피 차이로 정의됩니다.
◾ 엔트로피(Entropy)
데이터 세트 $S$의 엔트로피는 다음과 같이 계산된다.(많이 보았을 것이다)
$H(S) = - \sum_{i=1}^{n} p_i \log_2 p_i$
여기서, $p_i$는 데이터 세트 $S$ 내에서 클래스 $i$의 비율을 나타낸다.
◾ 정보 이득 계산
feature $A$에 대한 정보 이득은 다음과 같이 계산된다.
$IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)$
여기서, $IG(S, A)$는 fature $A$를 사용하여 데이터 세트 $S$를 분할했을 때의 정보 이득.
$H(S)$는 원래 세트의 엔트로피, $Values(A)$는 속성 $A$가 취할 수 있는 모든 값들의 집합.
$|S_v|$는 속성 $A$의 값이 $v$일 때의 세트 크기, $H(S_v)$는 속성 $A$의 값이 $v$일 때의 세트의 엔트로피를 나타낸다.
ID3 알고리즘은 이 정보 이득을 최대화하는 속성을 찾아 해당 속성으로 데이터 세트를 분할한다.
이러한 방법을 feature A뿐 아닌 모든 feature에 대해 반복 계산하고 $IG$(information gain)을 최대화 하는 feature를 선택하여 분할한 후, 다음 단계에서 다른 feature들로 반복해나가는 것이다.
앞서 보았던 파이썬 예시는 gini 계수로 CART 알고리즘을 활용한 것이다. 파이썬에서 완벽한 ID3 알고리즘을 구현하지는 않아도 분류기준을 entropy로 바꾸어 구현해볼 수 있다.
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
# 데이터 불러오기
iris = load_iris()
X, y = iris.data, iris.target
# 의사결정 나무 모델 생성 (ID3 비슷한 방식으로)
# 'entropy' 기준을 사용해 엔트로피를 기반으로 하는 의사결정 나무 생성
dt_clf = DecisionTreeClassifier(criterion='entropy')
dt_clf.fit(X, y)
# 모델의 결정 트리 시각화
plt.figure(figsize=(20,10))
plot_tree(dt_clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names, rounded=True)
plt.show()
확인해 보면 앞서 보았던 그림과 다르게 gini가 아닌 entropy가 사용된 것을 볼 수 있다!
◾ 장단점
ID3 알고리즘의 장점은 매우 직관적으로 생각보다 패턴을 잘 식별한다는 점이다.(특히 범주형에서) 또한 계산 비용이 적다.
단점이라함은, 과적합의 위험이 크고 연속형 변수처리가 어렵다. 또한 불균형 데이터와 결측치 데이터에 민감하고 처리하기 어렵다.
◼️ CART(Calssification and Regression Trees) 알고리즘
CART의 경우 앞선 포스팅에서 다룬 적이 있었다. ID3 알고리즘과의 차이와 구별점을 보기위해 다시한번 알아보자.
CART(Classification and Regression Trees) 알고리즘은 분류 및 회귀 문제에 사용될 수 있는 결정 트리 모델을 구축하기 위한 방법론이다.
1984년 Leo Breiman, Jerome Friedman, Richard Olshen, 그리고 Charles Stone에 의해 소개된 이 알고리즘은 데이터를 두 개의 하위 그룹으로 반복적으로 분할하여 트리를 구성한다.(찾아보니 논문이 아닌 서적이여서 찾기가 힘드네요 ㅜㅜ)
CART는 분류 문제(Classification)와 연속적 값을 예측하는 회귀 문제(Regression) 모두에 적용될 수 있는 범용적인 모델이다.
여기서 알 수 있는 ID3와의 차이점은 2가지로 첫 번째는 ID3와 다르게 CART는 하나의 노드에 대한 하위노드가 2개입이다. 즉, 분할은 꼭 양갈래로만 이루어 진다는 점. 그리고 두 번째는 ID3와 다르게 회귀 문제에서도 적용가능 하다는 점이다.
◾ CART의 핵심 원리
CART 알고리즘은 특정 속성에 대한 최적의 분할을 찾기 위해 불순도(impurity) 또는 오차(error) 기준을 사용하는데, 이러한 기준은 문제의 유형(분류 또는 회귀)에 따라 달라진다.
분류 문제의 경우, CART는 주로 지니 불순도(Gini Impurity)를 사용한다.(엔트로피(Entropy)를 사용할 수도 있다)
지니 불순도의 계산을 아래와 같다.
$Gini(S) = 1 - \sum_{i=1}^{n} p_i^2$
여기서, $p_i$는 ID3에서 본 것과 같이 특정 클래스에 속하는 데이터 포인트의 비율을 나타냅니다.
회귀 문제의 경우, CART는 데이터 포인트와 분할 후 각 그룹의 평균 간의 평균 제곱 오차(Mean Squared Error, MSE) 또는 평균 절대 오차(Mean Absolute Error, MAE)를 최소화하는 방식으로 분할을 결정합니다.
◾ 분할 과정
1. 최적의 분할 찾기: CART는 각 단계에서 모든 가능한 분할을 평가하고, 가장 높은 불순도 감소(분류) 또는 오차 감소(회귀)를 제공하는 분할을 선택한다.(ID3와 같이 모든 feature와 모든 분리기준을 사용)
2. 재귀적 분할 : 선택된 최적의 분할을 사용하여 데이터를 두 하위 그룹으로 분할한 다음, 이 과정을 각 하위 그룹에 대해 반복적으로 수행한다. 이 과정은 더 이상 분할이 불가능하거나 사용자가 설정한 트리의 최대 깊이에 도달할 때까지 계속된다.(ID3와 같이 이를 반복한다)
3. 가지치기(Pruning) : 과적합을 방지하기 위해, CART는 생성된 트리를 가지치기하는 과정을 포함한다. 이는 복잡한 트리에서 일부 노드를 제거하여 더 간단한 모델을 만드는 과정을 의미한다.
해당 가지치기가 ID3와 비교되는 차이점이다. ID3와 다르게 CART에서는 과적합 방지를 위해 너무나 광범위하고 세부적인 나무의 가지를 잘라서 간결하고 일바화 가능성이 높은 나무를 생성하는 것입니다.
이에 대한 내용은 이미 포스팅 한 적이 있으니 한번 확인해보시면 좋을 것 같습니다. (링크 : 프루닝)
📌 정리
ID3 그리고 CART에 대해 알아보았습니다. 이 전에 ID3의 한계점을 조금이나마 극복하기 위해 개발된 C4.5 알고리즘도 있으나, 본 포스팅에서 다루진 않았습니다. ID3와 비슷한 방법으로 찾아보면 이해하기 쉬울 것입니다!
현직이 아닌 공부하는 사람으로서 자세히 알지는 모르지만 대부분의 트리 구조 모델에서 CART 알고리즘을 사용하는 것 같더군요. 앞서 포스팅에서도 보았지만 ID3에 비해 과적합면에서도 상위 버전이고 회귀에서도 적용된다는 점이 클 것 같습니다. 또한 CART 알고리즘은 타 알고리즘과 다르게 통계학 분야에서 만들어졌다고 합니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
|---|---|
| 조건부 추론 나무(Conditional Inference Trees) (0) | 2024.02.19 |
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
| 앙상블(Ensemble) : Voting model(Hard, Soft, Weighted) (1) | 2023.12.07 |
| ROC, AUC (ROC curve 그리는 법) (2) | 2023.12.05 |
