수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 Regression Trees
ML에 있어서 우리는 데이터를 사용하여 모델을 훈련시킵니다. 이 모델을 사용하여 새로운 데이터에 대한 예측을 하려하죠.
이때 예측하려는 데이터의 공간을 작은 부분들로 나누어 예측합니다.

${R_1, ..., R_k}$를 예측변수 공간 $\chi = {(x_1,...,x_p)}$의 파티션이라고 한다면, 아래와 같은 공간 함수를 고려합니다.
$$
f(\textbf{x}) = \sum_{j=1}^K \beta_j I(\textbf{x} \in R_j)
$$
여기서 $I(\textbf{x} \in R_j)$는 $\textbf{x}$가 공간 $R_j$에 속하는지 여부를 나타내는 함수 입니다.
문제는 어떻게 공간 $R_j$와 계수 $\beta_j$를 알 수 있는가 입니다.
이때 재귀적 이진 분할 알고리즘(recursive binary splitting algorithm)을 사용합니다. 또한, $\beta_j$는 $R_j$ 내의 관측치 응답 값의 평균으로 추정될 수 있습니다.
이를 바로 회귀 트리 방법이라고 합니다. 한번 자세히 봅시다.
재귀적 이진 분할 알고리즘(recursive binary splits algorithm)
임의의 주어진 직사각형 공간 $R$이 있을 때, $R_1 = \{ \textbf{x} : x_j \leq a_j \}$, $R_2 = \{ \textbf{x} : x_j \geq a_j \}$을 고려해야 합니다. 이 하위 직사각형들이 바로 $x_j, a_j$에 의해 결정 됩니다.
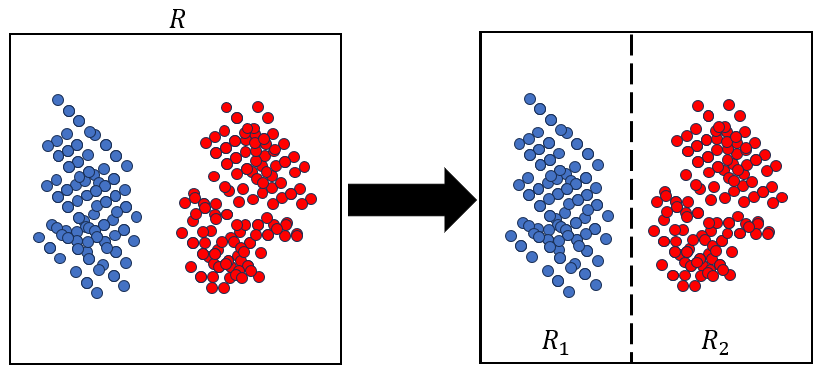
그럼 이 경계를 어떻게 결정할까요? 바로 아래 식의 $\Delta I$를 최대화하는 값을 찾는 것 입니다.
$$\Delta I(R, R_1, R_2) = \sum_{\textbf{x}_k \in R}(y_k - \bar{y}_R)^2 - [\sum_{\textbf{x}_k \in R_1}(y_k - \bar{y}_{R_1})^2 + \sum_{\textbf{x}_k \in R_2}(y_k - \bar{y}_{R_2})^2]$$
식을 보면 전체 공감에서의 예측값과 실제값의 차의 제곱. 즉 전체공간에서의 RSS입니다. 해당 값에 $R_1$ 공간에서의 RSS, $R_2$ 공간에서의 RSS를 합친 후 빼준 값이 최대가 되어야 합니다.
이 $\Delta I$가 최대가 되려면 $R_1, R_2$ 공간에서의 RSS가 최대한 작아야 합니다. 이 말은 즉, 각 부분 공간에서 모델의 예측이 실제값과 최대한 같아야한다는 것과 같습니다.

이제 이 방법을 특정 stopping rule이 만족할 때 까지 반복합니다.
흔한 stopping rule로는 사각형 안의 관측치의 최소 개수를 정하는 것입니다. 예를 들어 10으로 정했다면, 하위 공간안에 5개의 값이 들어갔을 때 알고리즘을 멈추는 것입니다.
📌 R로 구현해보기.
R의 Boston 데이터를 이용하여 한번 구현해봅시다.
- 데이터 가져와 train, test set 7:3으로 나누기
library(MASS)
str(Boston)
set.seed(42)
n=dim(Boston)[1]
train=sample(n,n*0.7)
b_train = Boston[train,]
b_test = Boston[-train,]- 트리 적용하기
library(tree)
bt = tree(medv~., data=b_train)
plot(bt)
text(bt)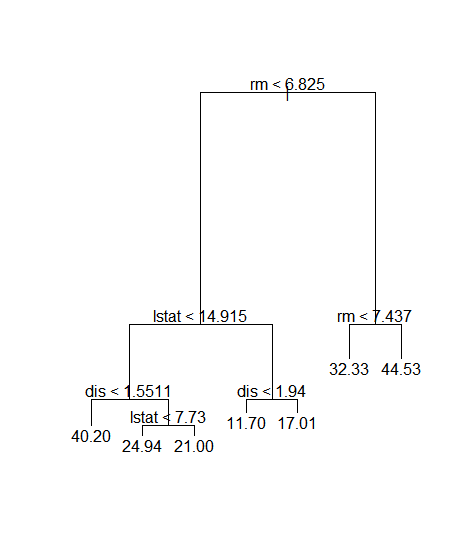
그림을 보시면 직관적으로 이해할 수 있을 겁니다. 각각 변수에따라 기준값도 알려줍니다. 이는 tree 모델이 설명력이 좋은 이유 중 하나입니다.
- tree regression의 RSS
한번 RSS값을 봅시다.
pred.bt = predict(bt, b_test)
mean((pred.bt-b_test$medv)^2)
>> 26.62757대략 26.627이 나왔습니다. 그럼 tree 모델이 아닌 단순한 linear model로 한다면 RSS가 다를까요?
- linear model의 RSS
bl = lm(medv~., data=b_train)
pred.bl = predict(bl, b_test)
mean((pred.bl-b_test$medv)^2)
>> 20.17313보시면 알겠지만 LM 모델의 RSS가 더 낮습니다, 단순한 선형 회귀임에도 tree보다 성능이 좋음을 알 수 있습니다.
이게 단순 CART 모델의 문제점입니다. 어떠한 통계적 모델이 아닌 단순 알고리즘 모델이기 때문에 performance가 좋진 않습니다만, 직관적이고 단순하며 설명력이 좋은게 장점입니다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| 3. Bagging(배깅) : Random Forest은 뭐가 다를까? (0) | 2023.10.12 |
|---|---|
| 2. Bagging(배깅) : Out of bag error estimation (0) | 2023.10.12 |
| 1. Bagging(배깅) : 왜 여러 모델을 쓰는가? (0) | 2023.10.10 |
| Pruning(프루닝, 가지치기) with Tree model (0) | 2023.10.10 |
| CART 2. 분류나무(Classification tree)[지니 계수, 엔트로피] (0) | 2023.10.09 |
