수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
자주 보이는 성능 지표는 아니지만 분류 목적에 있어서 가끔 사용되는 plot중 하나로 calibration plot이 있다.
Calibration plot(캘리브레이션 플롯)은 머신러닝 모델의 예측 정확도와 신뢰도를 시각적으로 평가하는데 사용되는 도구이다.
모델이 예측한 확률과 실제 결과 간의 일치 정도를 평가함으로써, 모델의 성능을 직관적으로 이해할 수 있게 해준다. 특히, 분류 문제에서 모델의 예측 확률이 실제 발생 확률과 얼마나 잘 맞는지를 검증함으로써, 모델의 신뢰성을 검증 할 수 있다.
📌 Calibration plot
우선 우리가 적합한 모델이 있다고 가정합시다. 그렇다면 이 모델로 인하여 나온 데스트 세트의 각 샘플에 대한 예측 확률이 계산되었을 것이다.(분류니까 각 클래스에 속할 확률이라고 하자)
예시 그래프와 함께 설명해보자.
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.calibration import calibration_curve, CalibratedClassifierCV
import matplotlib.pyplot as plt
# 예시 데이터 생성
X, y = make_classification(n_samples = 1000, n_features=20, n_classes=2,
random_state=42)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 적합
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)
# 예측 확률 계산
probs_pos = model.predict_proba(X_test)[:,1]
# 플롯 생성을 위한 실제 확률과 예측 확률
true_prob, predicted_prob = calibration_curve(y_test, probs_pos, n_bins=10)
# 캘리브레이션 플롯 그리기
plt.plot(predicted_prob, true_prob, marker='o', linewidth=1, label = 'Logistic Regression')
plt.plot([0,1], [0,1], linestyle='--', label = 'Perfectly calibrated')
plt.xlabel('Mean predicted probability')
plt.ylabel('Fraction of positives')
plt.title('Calibration plot')
plt.legend()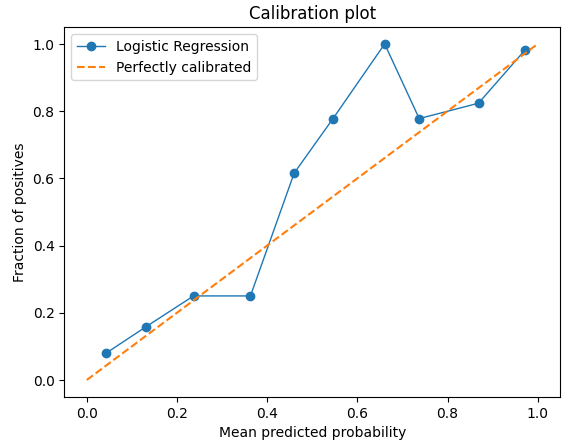
파이썬 코드로 y 클래스가 2개인 예시 데이터 1000개를 생성하였고, 로지스틱 회귀를 사용하여 분류하였다. 이를 이용해서 만들 Calibration plot이다.
1. x축 구간 나누기
: 우선 x축의 구간을 나눈다. 위 코드에서 'calibration_curve(n_bins=10)'으로 한 것처럼 x 축의 구간을 몇개로 나눈다.
위를 예시로 들면 0.0 부터 1.0 까지 0.1 의 간격으로 나누는 것.
2. 구간별 평균 예측 확률과 실제 빈도 비교
: 각 구간에 대해 모델이 예측한 확률의 평균과 해당 구간에서의 실제 결과 빈도(실제 발생 확률)을 계산한다.
위의 예시에서 0.2~0.3에 데이터를 보자. 이 구간의 샘플들은 1로 분류될 확률이 0.2~0.3인 샘플들이다.
이 확률에 의거하면 해당 구간에 있는 샘플들의 약 20%~30%만이 1로 분류되어야 한다. 예시 그래프의 y축 값을 보면? 실제로 약 0.2~0.3 사이에 있는 것을 확인할 수 있다. 때문에 분류가 아주 잘 이루어져 있는 것이라고 볼 수 있다.
반대로 0.6~0.7을 보면?? 대략 60%~70%가 1로 분류되어야하지만 거의 100%에 가깝게 1로 분류되었기 때문에 분류가 잘 이루어 지지 못한 것이라고 볼 수 있다.
3. 플롯 그리기
: 2 단계에서 설명한 것과같이 각 구간의 평균값과 실제 빈도간의 관계를 계산하여, x축에는 평균 예측 확률을, y축에는 실제 결과 빈도를 나타내는 그래프를 그리면 된다.
가장 좋은 분류 성능을 보이려면? 그래프가 y=x인 대각선에 가깝게 위치해야한다는 것.
이렇게 보면 굉장히 쉬운데, 처음 보게되면 이게 무슨 그래프인가... 싶다..
결국 이러한 접근 방법은 모델의 예측이 실제 샘플의 확률과 얼마나 잘 일치하는지를 평가하는데 중요한 역할이 될 수 있다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| CATboost 기본 특징 (0) | 2024.04.22 |
|---|---|
| 부분 의존성 플롯(Partial Dependence Plot, PD) 그리고 개별 조건부 평균 플롯(Individual Conditional Expectation Plot, ICE) (1) | 2024.02.27 |
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
자주 보이는 성능 지표는 아니지만 분류 목적에 있어서 가끔 사용되는 plot중 하나로 calibration plot이 있다.
Calibration plot(캘리브레이션 플롯)은 머신러닝 모델의 예측 정확도와 신뢰도를 시각적으로 평가하는데 사용되는 도구이다.
모델이 예측한 확률과 실제 결과 간의 일치 정도를 평가함으로써, 모델의 성능을 직관적으로 이해할 수 있게 해준다. 특히, 분류 문제에서 모델의 예측 확률이 실제 발생 확률과 얼마나 잘 맞는지를 검증함으로써, 모델의 신뢰성을 검증 할 수 있다.
📌 Calibration plot
우선 우리가 적합한 모델이 있다고 가정합시다. 그렇다면 이 모델로 인하여 나온 데스트 세트의 각 샘플에 대한 예측 확률이 계산되었을 것이다.(분류니까 각 클래스에 속할 확률이라고 하자)
예시 그래프와 함께 설명해보자.
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.calibration import calibration_curve, CalibratedClassifierCV
import matplotlib.pyplot as plt
# 예시 데이터 생성
X, y = make_classification(n_samples = 1000, n_features=20, n_classes=2,
random_state=42)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 모델 적합
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)
# 예측 확률 계산
probs_pos = model.predict_proba(X_test)[:,1]
# 플롯 생성을 위한 실제 확률과 예측 확률
true_prob, predicted_prob = calibration_curve(y_test, probs_pos, n_bins=10)
# 캘리브레이션 플롯 그리기
plt.plot(predicted_prob, true_prob, marker='o', linewidth=1, label = 'Logistic Regression')
plt.plot([0,1], [0,1], linestyle='--', label = 'Perfectly calibrated')
plt.xlabel('Mean predicted probability')
plt.ylabel('Fraction of positives')
plt.title('Calibration plot')
plt.legend()
파이썬 코드로 y 클래스가 2개인 예시 데이터 1000개를 생성하였고, 로지스틱 회귀를 사용하여 분류하였다. 이를 이용해서 만들 Calibration plot이다.
1. x축 구간 나누기
: 우선 x축의 구간을 나눈다. 위 코드에서 'calibration_curve(n_bins=10)'으로 한 것처럼 x 축의 구간을 몇개로 나눈다.
위를 예시로 들면 0.0 부터 1.0 까지 0.1 의 간격으로 나누는 것.
2. 구간별 평균 예측 확률과 실제 빈도 비교
: 각 구간에 대해 모델이 예측한 확률의 평균과 해당 구간에서의 실제 결과 빈도(실제 발생 확률)을 계산한다.
위의 예시에서 0.2~0.3에 데이터를 보자. 이 구간의 샘플들은 1로 분류될 확률이 0.2~0.3인 샘플들이다.
이 확률에 의거하면 해당 구간에 있는 샘플들의 약 20%~30%만이 1로 분류되어야 한다. 예시 그래프의 y축 값을 보면? 실제로 약 0.2~0.3 사이에 있는 것을 확인할 수 있다. 때문에 분류가 아주 잘 이루어져 있는 것이라고 볼 수 있다.
반대로 0.6~0.7을 보면?? 대략 60%~70%가 1로 분류되어야하지만 거의 100%에 가깝게 1로 분류되었기 때문에 분류가 잘 이루어 지지 못한 것이라고 볼 수 있다.
3. 플롯 그리기
: 2 단계에서 설명한 것과같이 각 구간의 평균값과 실제 빈도간의 관계를 계산하여, x축에는 평균 예측 확률을, y축에는 실제 결과 빈도를 나타내는 그래프를 그리면 된다.
가장 좋은 분류 성능을 보이려면? 그래프가 y=x인 대각선에 가깝게 위치해야한다는 것.
이렇게 보면 굉장히 쉬운데, 처음 보게되면 이게 무슨 그래프인가... 싶다..
결국 이러한 접근 방법은 모델의 예측이 실제 샘플의 확률과 얼마나 잘 일치하는지를 평가하는데 중요한 역할이 될 수 있다.
'⚙️ Machine Learning > Machine learning' 카테고리의 다른 글
| CATboost 기본 특징 (0) | 2024.04.22 |
|---|---|
| 부분 의존성 플롯(Partial Dependence Plot, PD) 그리고 개별 조건부 평균 플롯(Individual Conditional Expectation Plot, ICE) (1) | 2024.02.27 |
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
| 불균형 데이터(Imbalanced Data) 처리 : 임계값(threshold) 조정 (0) | 2024.02.21 |
