수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
우리가 예측을 할 때, 예측력이 높은 것도 중요하지만 주제와 목적에 따라 모델의 내부 메커니즘을 이해하는 것도 중요할 수 있습니다.
모델이 어떻게 특정 변수에 의존하는지, 즉 특정 input과 output간의 관계가 어떻게 이루어져 있는지 이해하는 것이 모델을 해석하는 데 중요할 수 있가다는 것입니다. 이러한 맥락에서 부분 의존성 플롯(PD)와 개별 조건부 평균 플롯(ICE)은 중요한 역할을 할 수 있습니다.
부분 의존성 플롯(PD)는 데이터 세트 내의 하나 또는 두 개의 특성과 예측 결과 사이의 관계를 시각화 합니다. 특정 특성의 다양한 값들이 예측 결과에 어떻게 영향을 미치는지 보여줌으로써, 모델이 특성을 어떻게 해석하는지에 대한 통찰력을 제공합니다.
반면, 개별 조건부 평균 플롯(ICE)는 각 관측치에 대한 예측값이 특성의 변화에 따라 어떻게 달라지는지를 보여줍니다. 어찌보면 PD와 비슷하지만? 개별 관측치 수준에서 특성의 영향을 보여주며 모델 예측의 변동성과 개별성을 탐색할 수 있게 합니다.
이러한 맥락에서 PD는 전역 해석(global), ICE는 지역 해석(local)이라고 불 수 있습니다.
이렇게 말로 설명하면 어려우니 직접 한번 확인해봅시다.
📌 부분 의존성 플롯(Partial Dependence Plot. PD)
PD는 앞서 설명한 것 처럼, 하나 또는 두 개의 입력 변수가 예측 결과에 미치는 평균적인 영향을 시각화하는 도구이다.
특정 변수가 우리가 예측하려는 변수에 미치는 영향을 이해하기 위해 사용한다.
PD는 다른 모든 변수를 고정시킨 상태에서 관심 있는 변수의 다양한 값들에 대해 예측한 결과의 평균을 통해 생성된다.
◼️ 부분 의존성 함수
$$
PD(x_S) = \dfrac{1}{N} \sum^{N}_{i=1}f(x_S, s^i_c)
$$
여기서 :
- $x_S$ 는 관심 있는 feature의 값
- $x^i_c$ 는 고정된 다른 feature들의 값
- $N$ 은 데이터 포인트의 총 개수
- $f()$는 머신러닝 모델의 예측 함수
이 식은 우리가 관심 있는 특정 feature $x_S$에 대한 모델의 예측값이 $x_S$의 각각의 값에 대한 다른 모든 특징 $x_c$를 고려하여 어떻게 변하는지 평균적인 영향을 계산한다.
이 평균은 $x_S$의 모든 가능한 값에 대해 계산되고 결과적으로 $x_S$와 예측하려는 변수 사이의 관계를 나타내는 곡선이 생성된다.
◼️ 계산 과정
1. feature 공간 탐색 : 관심 있는 feature $x_S$의 가능한 모든 값들을 대상으로 예측을 수행한다. 이 때, 다른 모든 feature들은 각 데이터 포인트에 대해 원래 본인의 값을 유지한다.
2. 평균 예측값 계산 : 위에서 언급한 수식에 따라, 각 $x_S$에 대해 평균 예측값을 계산한다.
3. 그리기 : $x_S$ 값들에 대응하는 평균 예측값을 이용하여 그래프를 그린다.
그렇다면 한번 그려보자.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.inspection import PartialDependenceDisplay
# 데이터 생성
X, y = make_friedman1(n_samples=1000, n_features=10, random_state=42)
# 모델 적합
model = GradientBoostingRegressor(random_state=42)
model.fit(X,y)
# 부분 의존성 플롯 생성
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.inspection import PartialDependenceDisplay
# 데이터 생성
X, y = make_friedman1(n_samples=1000, n_features=10, random_state=42)
# 모델 적합
model = GradientBoostingRegressor(random_state=42)
model.fit(X,y)
# 부분 의존성 플롯 생성
display = PartialDependenceDisplay.from_estimator(model, # 학습 모델
X, # 데이터
[0], # 관심 변수
kind = 'average' # average = PD, individual = ICE
)
plt.title('Partial Dependence Plot')
plt.show()
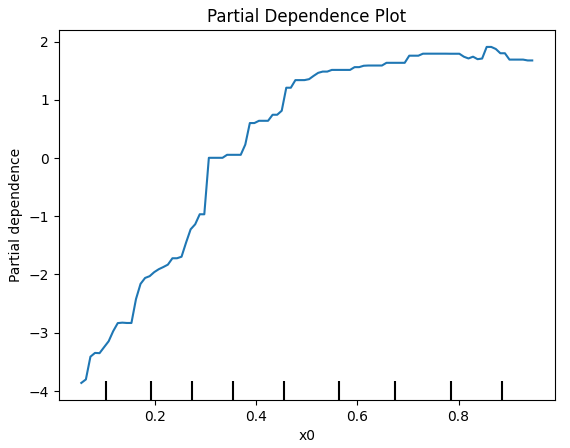
파이썬 코드로 1000개의 데이터 샘플을 만들었고, 총 10개의 feature가 있다. 이를 그라디언트 부스팅을 통해 학습시켰고, 1 번째 feature의 PD를 확인하였다. 1 번째 feature와 예측하고자 하는 변수 y의 관계를 이렇게 확인할 수 있다.
◼️ 한계점
1. 개별 데이터 포인트 무시
PD의 한계점은 명확하다. 앞서 PD는 전역 해석과 관련있다.
PD 플롯은 특정 feature에 대해 모델의 평균적인 반응만을 보여주기 때문에, 각각의 개별 데이터 포인트에서 관찰될 수 있는 예측값의 변화는 확인 할 수 없다.
2. 비선형성과 복잡성에 대한 제한된 시각화
PD는 모델의 평균적인 영향을 단순화하여 보여주기 때문에, 모델의 비선형성이나 복잡한 동작을 완전히 포착하지 못할 수 있다. 특히, 모델이 데이터의 특정 영역에서 예상치 못한 방식으로 동작하는 경우, 이러한 세부 사항은 PD 플롯에서 표현하기 어렵다.
예를 들면, 우리가 앞서 살펴본 데이터의 1 번째 feature가 0.0~0.6 까지 범위가 끝이라고 할때, 적합한 모델에 0.9의 값이 들어갈 경우 예측값은 과연 정확한 예측값일까? 그렇지 않을 수 있다.
이렇게 PD에서 데이터 포인트가 없는 부분으로 기대 곡선이 표현되는 것을 외삽(extrapolation)이라고 한다.
이러한 단점을 극복하기 위해 개별 조건부 기대값(Individual Conditional Expectation, ICE) 플롯이 사용된다.
📌 개별 조건부 기대값 플롯(Individual Conditional Expectation, ICE)
ICE는 평균이 아닌 각각의 데이터 포인트에 대해 모델의 예측이 특정 특징의 값에 따라 어떻게 변화하는지를 시각화함으로써, PD 플롯이 제공하지 못하는 세부적인 것을 볼 수 있다.
◼️ ICE 플롯 함수
$$
ICE^i = f(x_S, x_c^i)
$$
여기서 :
- $ICE^i$ 는 i 번째 데이터 포인트에 대한 개별 조건부 기대값
- $x_S$ 는 관심 있는 feature 값
- $x_c^i$ 는 고정된 나머지 feature들의 값
- $f()$ 는 머신러닝 모델의 예측 함수
이 수식은 특정 데이터 포인트 $i$에 대해, 관심 있는 feature $x_S$의 값을 변화시키면서 모델의 예측값 $f(x_S, x_c^i)$를 계산한다.
이 과정을 데이터 세트의 모든 데이터 포인트에 대해 반복하고, 각 데이터 포인트에 대한 모델의 반응을 별도의 라인으로 그래프에 표시한다.
◼️ 계산 과정
1. feature 공간 탐색 : 관심 있는 feature $x_S$의 값 범위를 정의
2. 모델 반응 계산 : 각 데이터 포인트 $i$에 대해, $x_S$의 모든 가능한 값에 대한 모델의 예측값 $f(x_S, x_c^i)$를 계산
3. 플롯 그리기 : 각 데이터 포인트에 대해 계산된 모델의 예측값을 사용하여 ICE 플롯을 생성. 각 라인은 $x_S$의 값에 따른 하나의 데이터 포인트의 모델 예측값 변화를 보여줌.
한번 그려보면
# 개변 조건부 기대값 플롯 생성
PartialDependenceDisplay.from_estimator(model, # 학습 모델
X, # 데이터
[0], # 관심 변수
kind='individual', # average = PD, individual = ice
)
plt.title('Individual Conditional Expectation plot')
plt.show()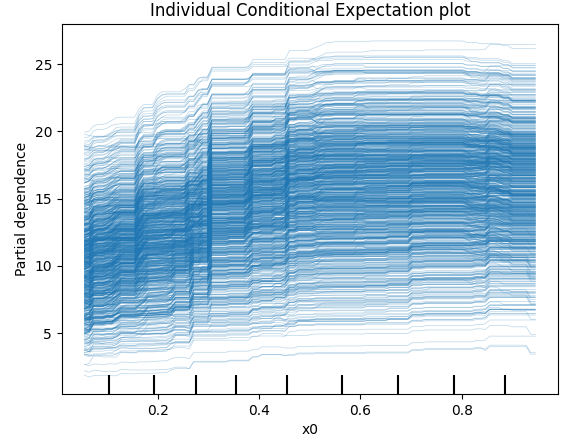
좀 더 편하게 보기위해 함수 안의 kind를 both로 설정하면 아래와 같이 PD와 ICE를 볼 수 있다.
# PD and ICE
PartialDependenceDisplay.from_estimator(model, # 학습 모델
X, # 데이터
[0], # 관심 변수
kind='both', # average = PD, individual = ice
)
plt.title('PD and ICE')
plt.show()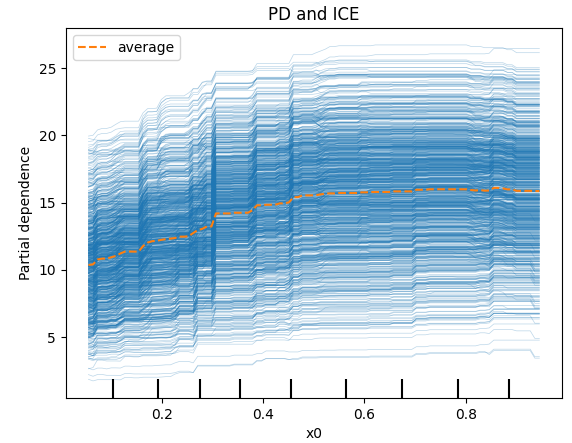
📌 중요한 이유..?
이렇게 PD와 ICE에 대해 살펴보았다, 그럼 이들의 차이가 왜 중요할까??
앞서 살펴본 예시에서는 이 들의 중요성이 크게 드러나지 않았지만 PD는 평균!을 이용한다는 점이 중요하다. 매우 극단적인 예시지만 PD와 ICE가 각각 아래와 같다면?? 어떻게 해석해야할까?
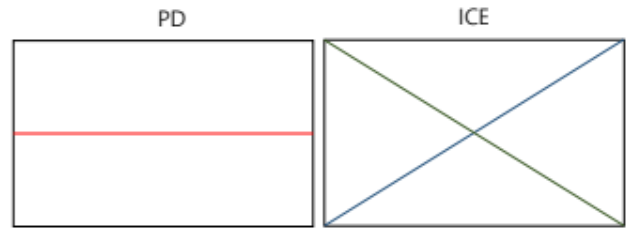
이러한 결과를 어떻게 해석해야 할것인가가 매우 중요한 부분이다. PD를 보면서 우리가 관심있는 feature는 결과 변수와 아무런 관련이 없다고 해석해야 할까? 혹은 ICE를 보면서 관련이 크다고 해야할까?
아마 제일 좋은 방법은 ICE를 보며 왜 저런 극단적인 결과가 나왔는지 기울기가 다른 각각의 샘플의 추가적인 차이를 확인해야 할것이다.
꼭 이러한 예시가 아니더라도, 결과 변수와 관심있는 변수간의 관계를 볼 수 있는 방법이기에 feature importance를 보는 것과는 또다른 의미가 있을 것이다.
'🌞 Statistics for AI > Machine learning' 카테고리의 다른 글
| 가우시안 혼합 모델(Gaussian Mixture model, GMM) (0) | 2024.04.25 |
|---|---|
| CATboost 기본 특징 (0) | 2024.04.22 |
| Calibration Plot 과 성능 확인 (0) | 2024.02.27 |
| 불균형 데이터(Imbalanced Data) 처리 : SMOTE, ADASYN (1) | 2024.02.23 |
| 불균형 데이터(Imbalanced Data) 처리 : 오버 샘플링(over sampling), 언더 샘플링(under sampling) (0) | 2024.02.21 |
