수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 정규 분포 (Normal distridution)
통계를 한다면 어쩌면 가장 많이 듣지 않을까 하는 분포 중 하나인 정규 분포 입니다. 보통 수학의 분야에선 Normal distribution(정규 분포)라고 하는데, 공학쪽 에서는 Gaussian Distribution(가우시안 분포)라고 하는 것 같더라구요. 처음엔 저도 헷갈렸습니다.
우리가 진행하는 많은 통계적 분석(T-test, F-test) 등등 모두 정규분포의 성질을 활용, 가정하여 분석하게 됩니다. 정말 중요한 분포이죠.
정규분포는 bell shape(종 모양)을 띄며 양 끝 꼬리로 갈 수록 낮아지고 평균과 가까울 수록 높아지는 모양을 보입니다. 또한 분산이 커질 수록 평평한 모양을 띄고, 분산이 작을 수록 뾰족한 모양에 가깝습니다.
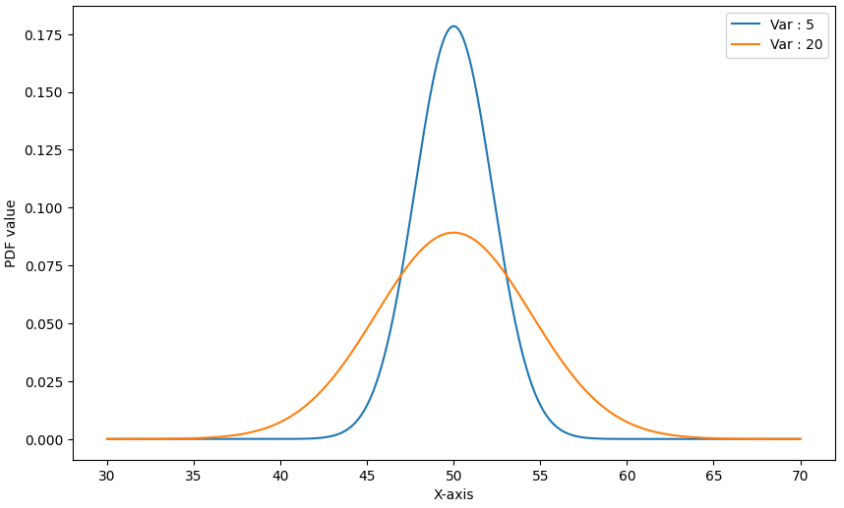
위 그래프에서 파란선은 분산이 5, 주황선은 분산이 20입니다. 분산이 클수록 평평해지는 것을 볼 수 있죠?
➕ 정규 분포의 확률 밀도 함수
정규분포의 확률 밀도 함수(PDF)는 두 개의 파라미터인 평균과 분산에 의해 정해집니다.
$$
f(x) = \dfrac{1}{\sigma \sqrt{2 \pi}} \exp \left[ -\dfrac{(x-\mu)^2}{2\sigma^2} \right], \ \ -\infty<x<\infty
\\ X \sim N(\mu, \sigma^2)
$$
📌 표준화 (Strandardization)
표준화를 왜 하는지를 이해하는 것이 중요합니다. 가장 많이 쓰이는 예시가 바로 수학 점수인데요.
X반과 Y반이 있습니다. X반은 평균이 70, 표준편차가 20이고, Y반은 평균이 80, 표준편차가 5라고 해봅시다.
X반의 75점과 Y반의 75점 중 어느 반에서 75점 맞은 것이 더 수학 점수가 높은 것일까요?
이 때, 표준화를 통해 점수를 비교할 수 있습니다.
표준화는 평균이 0, 표준편차를 1이 되도록 만들어 서로 다른 분포에서의 값을 비교하도록 할 수 있습니다.
표준화 점수는 아래와 같으며, 흔히 Z-score라고 합니다.
$$
Z = \dfrac{X-\mu}{\sigma}
$$
➕ 평균과 분산 유도
앞서 표준화를 통하여 평균 = 0, 표준편차 = 1 로 만든다고 하였는데 그럼 실제 $Z$ score의 평균과 분산을 구해봅시다.
- 평균
$$
E(Z) = E(\dfrac{X-\mu}{\sigma}) = \dfrac{1}{\sigma}[E(X)-\mu] = 0
$$
- 분산
$$
\begin{align}
Var(Z) &= Var(\dfrac{X-\mu}{\sigma}) = \dfrac{1}{\sigma^2}Var(X-\mu)
\\ &= \dfrac{1}{\sigma^2}Var(X) = 1
\end{align}
$$
📌 표준정규분포 (Strand Normal Distribution)
이렇게 정규분포를 표준화해서 얻은 분포를 표준정규분포라고 합니다. 아래와 같이 평균=0, 표준편차=1인 정규 분포를 따르는 것이죠.
$$
Z \sim N(0,1)
$$
➕ 표준 정규 분포의 확률 밀도 함수
표준 정규 분포의 확률 밀도 함수는 정규분포 확률밀도 함수에서 평균과 표준편차에 각각 0,1을 대입하면 되겠죠?
$$
f(z) = \dfrac{1}{\sqrt{2\pi}} \exp(-\dfrac{x^2}{2})
$$
'📊 Statistics for Basic > Distribution(분포)' 카테고리의 다른 글
| 표본 분산의 확률 분포가 카이제곱 분포인가 (0) | 2023.11.25 |
|---|---|
| 카이제곱 분포 (Chi-squared distribution) (1) | 2023.11.25 |
| 연속균등 분포 평균, 분산 증명 (1) | 2023.11.25 |
| 연속균등 분포 (Continous uniform distribution) (1) | 2023.11.25 |
| 푸아송 분포 평균, 분산 증명 (0) | 2023.11.25 |
📌 정규 분포 (Normal distridution)
통계를 한다면 어쩌면 가장 많이 듣지 않을까 하는 분포 중 하나인 정규 분포 입니다. 보통 수학의 분야에선 Normal distribution(정규 분포)라고 하는데, 공학쪽 에서는 Gaussian Distribution(가우시안 분포)라고 하는 것 같더라구요. 처음엔 저도 헷갈렸습니다.
우리가 진행하는 많은 통계적 분석(T-test, F-test) 등등 모두 정규분포의 성질을 활용, 가정하여 분석하게 됩니다. 정말 중요한 분포이죠.
정규분포는 bell shape(종 모양)을 띄며 양 끝 꼬리로 갈 수록 낮아지고 평균과 가까울 수록 높아지는 모양을 보입니다. 또한 분산이 커질 수록 평평한 모양을 띄고, 분산이 작을 수록 뾰족한 모양에 가깝습니다.

위 그래프에서 파란선은 분산이 5, 주황선은 분산이 20입니다. 분산이 클수록 평평해지는 것을 볼 수 있죠?
➕ 정규 분포의 확률 밀도 함수
정규분포의 확률 밀도 함수(PDF)는 두 개의 파라미터인 평균과 분산에 의해 정해집니다.
$$
f(x) = \dfrac{1}{\sigma \sqrt{2 \pi}} \exp \left[ -\dfrac{(x-\mu)^2}{2\sigma^2} \right], \ \ -\infty<x<\infty
\\ X \sim N(\mu, \sigma^2)
$$
📌 표준화 (Strandardization)
표준화를 왜 하는지를 이해하는 것이 중요합니다. 가장 많이 쓰이는 예시가 바로 수학 점수인데요.
X반과 Y반이 있습니다. X반은 평균이 70, 표준편차가 20이고, Y반은 평균이 80, 표준편차가 5라고 해봅시다.
X반의 75점과 Y반의 75점 중 어느 반에서 75점 맞은 것이 더 수학 점수가 높은 것일까요?
이 때, 표준화를 통해 점수를 비교할 수 있습니다.
표준화는 평균이 0, 표준편차를 1이 되도록 만들어 서로 다른 분포에서의 값을 비교하도록 할 수 있습니다.
표준화 점수는 아래와 같으며, 흔히 Z-score라고 합니다.
$$
Z = \dfrac{X-\mu}{\sigma}
$$
➕ 평균과 분산 유도
앞서 표준화를 통하여 평균 = 0, 표준편차 = 1 로 만든다고 하였는데 그럼 실제 $Z$ score의 평균과 분산을 구해봅시다.
- 평균
$$
E(Z) = E(\dfrac{X-\mu}{\sigma}) = \dfrac{1}{\sigma}[E(X)-\mu] = 0
$$
- 분산
$$
\begin{align}
Var(Z) &= Var(\dfrac{X-\mu}{\sigma}) = \dfrac{1}{\sigma^2}Var(X-\mu)
\\ &= \dfrac{1}{\sigma^2}Var(X) = 1
\end{align}
$$
📌 표준정규분포 (Strand Normal Distribution)
이렇게 정규분포를 표준화해서 얻은 분포를 표준정규분포라고 합니다. 아래와 같이 평균=0, 표준편차=1인 정규 분포를 따르는 것이죠.
$$
Z \sim N(0,1)
$$
➕ 표준 정규 분포의 확률 밀도 함수
표준 정규 분포의 확률 밀도 함수는 정규분포 확률밀도 함수에서 평균과 표준편차에 각각 0,1을 대입하면 되겠죠?
$$
f(z) = \dfrac{1}{\sqrt{2\pi}} \exp(-\dfrac{x^2}{2})
$$
'📊 Statistics for Basic > Distribution(분포)' 카테고리의 다른 글
| 표본 분산의 확률 분포가 카이제곱 분포인가 (0) | 2023.11.25 |
|---|---|
| 카이제곱 분포 (Chi-squared distribution) (1) | 2023.11.25 |
| 연속균등 분포 평균, 분산 증명 (1) | 2023.11.25 |
| 연속균등 분포 (Continous uniform distribution) (1) | 2023.11.25 |
| 푸아송 분포 평균, 분산 증명 (0) | 2023.11.25 |
