수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 Smoothing spline
smoothing spline(스무딩 스플라인)은 회귀 스플라인(링크 : 회귀 스플라인)과 유사하지만 약간 다른 상황에서 나탄나다. 이름에서 드러나는 것 처럼 잔차 제곱합 기준을 최소화 하면서 smoothness penalty(부드러움 패널티..?)를 고려하는 방식으로 생성된다.
이는 데이터에 부드러운 곡선을 적합시키는 통계적 방법 중 하나로, 데이터에 대한 복잡한 관계를 모델링하고자 할 때 사용된다. 잔차 최곱합을 최소화 하면서도? 부드러운 곡선을 유지하기 위해서 패널티 항을 추가한다는 얘기..
자유도를 가진 함수를 사용하여 데이터를 설명하고, 이 함수의 곡률, 기울기에 제약을 두어 부드러운 형태를 유지하는 방식을 사용. 즉! 우리가 조정해줄 하이퍼 파라미터가 존재한다는 이야기다.
아래와 같은 Loss term과 penalty term으로 이루어져 있다.
$$
RSS(f, \lambda) = \sum_{i=1}^N (y_i - f(x_i))^2 + \lambda \int(f''(t))^2dt
$$
이때의 이 식을 최소화하는 $f$를 스무딩 스플라인이라고 하고, $\lambda$는 당연히 하이퍼 파라미터로 우리가 튜닝해줘야할 파라미터이다. (첫 항 : 손실항, 두 번째 항 : 페널티 항)
$\lambda =0$ 이면?? $f$는 데이터를 보간(interpolate)하는 어떠한 함수일 것이고
$\lambda = \infty$ 이면?? 최소 자승 적합(least squares fit)일 것이다.
근데 여기서 페널티 항을 보면 신기한 형태를 보이는데, 2차 미분에다가 적분을 취해버린다.
이게 무슨 의미일까? 우선 $f''(t)$는 $f$의 2차 미분식인 것을 다들 알 것이다.
2차미분은? 기울기 변화량을 나타낸다. 변화량이 크다? 그러면 모형이 복잡하다는 것이고 $f''(t)$의 절댓값은 크다는 것. 모양이 단순할 수록 반대의 형태를 보일 것이다.
이들의 적분값이란??? 결국 이러한 변화량의 총합을 취한 것으로 볼 수 있다. 재밌네요.
결국 $\int(f''(t))^2 dt$ 값이 작다는 것은 모델이 단순하다(smooth)하다. 크다는 것은 모델이 복잡하다는 의미이고 이걸 $\lambda$라는 패널티항을 이용해 조정해주는 것!. $\lambda$값을 크게 설정할 수록 패널티가 커져 $f$는 더욱 간단한 모형이 될 것입니다.
위 식 $RSS(f,\lambda)$을 최소화하는 함수 $f$는 $x_1, ...,x_n$을 knots로 갖는 자연 큐빅 스플라인(natural cubic spline)과 같습니다. 근데 뭐 정확하게 동일하지는 않다고 하더군요. 축소 버전? 이라고 합니다.
◾ $\lambda$ 고르기
앞서 설명한 것과 같이 $\lambda$는 스무딩 스플라인의 튜닝 파라미터라고 하였습니다.
스무딩 스플라인에서의 자유도는 결국 $\lambda$가 관여하게 되는데.. 한번 보면 $\lambda = 0$이라고 둔다면 $df_\lambda=n$이 될것이다. 왜? 만약 패널티가 없다고 하면 모든 data point($x_1,...,x_n)$를 knot라고 둘 것이고? 이는 결국 모든 데이터 포인트를 fitting하는 함수를 추정하게 되는 꼴이기 때문.
그렇기 때문에 $\lambda$를 통해 이 $n$개의 매개변수를 제한하거나 축소할 수 있다.
아래식을 보면
$$
\hat{f}_{\lambda} = S_\lambda \cdot y
$$
이때 $\hat{f}$는 우리가 지정한 $\lambda$값에 대한 $RSS$식의 해이다.
결국? train set인 $x_1,...,x_n$에 대한 스무딩 스플라인의 값이라는 것. 그래서 $\hat{f}_\lambda$는 스무딩 스플라인에 fitting하여 나오는 값 $S_\lambda$ ( $n \times n$ 행렬)와 $y$값의 곱으로 표현되는 것.
이를 통해 자유도 $df_\lambda$를 표현하면 아래와 같다.
$$
df_\lambda = \sum_{i=1}^n (S_\lambda)_{ii}
$$
큐빅 스플라인 처럼 knot의 개수를 정해주는 것이 아닌 $\lambda$값을 정해주면 되기에 CV(교차 검증)을 통해 에러를 최소화하는 $\lambda$값을 정해주면 된다.
LOOCV(Leave one out CV) error 계산식은 아래와 같음.($-i$ : $i$ 관측치 뺀것... leave one out이니까)
$$
RSS_{CV}(\lambda) = \sum_{i=1}^n \left(y_i - \hat{f}_\lambda^{(-i)}(x_i)\right)^2 - \sum_{i=1}^n \left( \dfrac{y_i - \hat{f}_\lambda (x_i)}{1 - (S_\lambda)_{ii}} \right)^2
$$
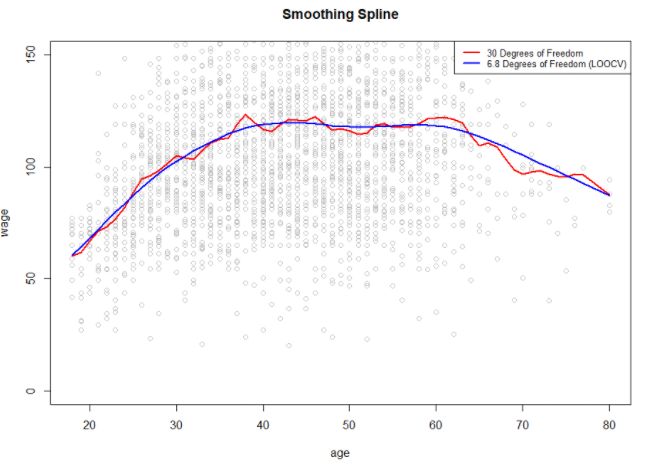
아래 그래프를 보면 빨간선은 임의로 자유도를 30으로 설정하여 복잡한 모델이 된것이고 파란선은 LOOCV를 통해 얻은 자유도인 6.8을 사용하여 만든 모델입니다.
'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| 로컬 스플라인(Local Spline) (1) | 2023.12.11 |
| 회귀 스플라인(Regression Spline) 그리고 Cubic spline? (1) | 2023.12.11 |
| 다항식 회귀(Polynomial regression) 그리고 계단 함수(Step function) (1) | 2023.12.07 |
📌 Smoothing spline
smoothing spline(스무딩 스플라인)은 회귀 스플라인(링크 : 회귀 스플라인)과 유사하지만 약간 다른 상황에서 나탄나다. 이름에서 드러나는 것 처럼 잔차 제곱합 기준을 최소화 하면서 smoothness penalty(부드러움 패널티..?)를 고려하는 방식으로 생성된다.
이는 데이터에 부드러운 곡선을 적합시키는 통계적 방법 중 하나로, 데이터에 대한 복잡한 관계를 모델링하고자 할 때 사용된다. 잔차 최곱합을 최소화 하면서도? 부드러운 곡선을 유지하기 위해서 패널티 항을 추가한다는 얘기..
자유도를 가진 함수를 사용하여 데이터를 설명하고, 이 함수의 곡률, 기울기에 제약을 두어 부드러운 형태를 유지하는 방식을 사용. 즉! 우리가 조정해줄 하이퍼 파라미터가 존재한다는 이야기다.
아래와 같은 Loss term과 penalty term으로 이루어져 있다.
$$
RSS(f, \lambda) = \sum_{i=1}^N (y_i - f(x_i))^2 + \lambda \int(f''(t))^2dt
$$
이때의 이 식을 최소화하는 $f$를 스무딩 스플라인이라고 하고, $\lambda$는 당연히 하이퍼 파라미터로 우리가 튜닝해줘야할 파라미터이다. (첫 항 : 손실항, 두 번째 항 : 페널티 항)
$\lambda =0$ 이면?? $f$는 데이터를 보간(interpolate)하는 어떠한 함수일 것이고
$\lambda = \infty$ 이면?? 최소 자승 적합(least squares fit)일 것이다.
근데 여기서 페널티 항을 보면 신기한 형태를 보이는데, 2차 미분에다가 적분을 취해버린다.
이게 무슨 의미일까? 우선 $f''(t)$는 $f$의 2차 미분식인 것을 다들 알 것이다.
2차미분은? 기울기 변화량을 나타낸다. 변화량이 크다? 그러면 모형이 복잡하다는 것이고 $f''(t)$의 절댓값은 크다는 것. 모양이 단순할 수록 반대의 형태를 보일 것이다.
이들의 적분값이란??? 결국 이러한 변화량의 총합을 취한 것으로 볼 수 있다. 재밌네요.
결국 $\int(f''(t))^2 dt$ 값이 작다는 것은 모델이 단순하다(smooth)하다. 크다는 것은 모델이 복잡하다는 의미이고 이걸 $\lambda$라는 패널티항을 이용해 조정해주는 것!. $\lambda$값을 크게 설정할 수록 패널티가 커져 $f$는 더욱 간단한 모형이 될 것입니다.
위 식 $RSS(f,\lambda)$을 최소화하는 함수 $f$는 $x_1, ...,x_n$을 knots로 갖는 자연 큐빅 스플라인(natural cubic spline)과 같습니다. 근데 뭐 정확하게 동일하지는 않다고 하더군요. 축소 버전? 이라고 합니다.
◾ $\lambda$ 고르기
앞서 설명한 것과 같이 $\lambda$는 스무딩 스플라인의 튜닝 파라미터라고 하였습니다.
스무딩 스플라인에서의 자유도는 결국 $\lambda$가 관여하게 되는데.. 한번 보면 $\lambda = 0$이라고 둔다면 $df_\lambda=n$이 될것이다. 왜? 만약 패널티가 없다고 하면 모든 data point($x_1,...,x_n)$를 knot라고 둘 것이고? 이는 결국 모든 데이터 포인트를 fitting하는 함수를 추정하게 되는 꼴이기 때문.
그렇기 때문에 $\lambda$를 통해 이 $n$개의 매개변수를 제한하거나 축소할 수 있다.
아래식을 보면
$$
\hat{f}_{\lambda} = S_\lambda \cdot y
$$
이때 $\hat{f}$는 우리가 지정한 $\lambda$값에 대한 $RSS$식의 해이다.
결국? train set인 $x_1,...,x_n$에 대한 스무딩 스플라인의 값이라는 것. 그래서 $\hat{f}_\lambda$는 스무딩 스플라인에 fitting하여 나오는 값 $S_\lambda$ ( $n \times n$ 행렬)와 $y$값의 곱으로 표현되는 것.
이를 통해 자유도 $df_\lambda$를 표현하면 아래와 같다.
$$
df_\lambda = \sum_{i=1}^n (S_\lambda)_{ii}
$$
큐빅 스플라인 처럼 knot의 개수를 정해주는 것이 아닌 $\lambda$값을 정해주면 되기에 CV(교차 검증)을 통해 에러를 최소화하는 $\lambda$값을 정해주면 된다.
LOOCV(Leave one out CV) error 계산식은 아래와 같음.($-i$ : $i$ 관측치 뺀것... leave one out이니까)
$$
RSS_{CV}(\lambda) = \sum_{i=1}^n \left(y_i - \hat{f}_\lambda^{(-i)}(x_i)\right)^2 - \sum_{i=1}^n \left( \dfrac{y_i - \hat{f}_\lambda (x_i)}{1 - (S_\lambda)_{ii}} \right)^2
$$
아래 그래프를 보면 빨간선은 임의로 자유도를 30으로 설정하여 복잡한 모델이 된것이고 파란선은 LOOCV를 통해 얻은 자유도인 6.8을 사용하여 만든 모델입니다.

'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| 로컬 스플라인(Local Spline) (1) | 2023.12.11 |
| 회귀 스플라인(Regression Spline) 그리고 Cubic spline? (1) | 2023.12.11 |
| 다항식 회귀(Polynomial regression) 그리고 계단 함수(Step function) (1) | 2023.12.07 |
