수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 로컬 회귀(Local Regression)
로컬 회귀 자체는 스플라인과 유사하지만 영역(region)들이 서로 겹치도록 허용되며, 이들 영역은 부드럽게 연결됩니다.
비모수 회귀 방법 중 하나로, 특히 데이터의 지역적인 패턴을 보고자 할 때 유용합니다. 기본적으로 특정 관측치 주변에서 회귀 모델을 만들어 해당 지역의 패턴을 파악하고, 이를 다른 지역과 겹치게 함으로써 전체 데이터에 대한 부드러운 회귀 모델을 형성합니다.
당연히 데이터가 지역적 특징을 가질 때 유용하고, 스플라인과 같은 전역적인 회귀모델은 전체 데이터에 대한 단일한 함수를 가정하지만, 로컬 회귀는 데이터의 지역적 특성을 놓치지 않고 볼 수 있습니다. 즉! 데이터가 비선형성이 강하고 지역적인 특이성을 파악하고자 할 때 사용합니다.
어떠한 target point ($x_0$) 근처의 관측치 만을 사용하여 함수의 적합을 해나갑니다.(메모리 기반 절차)

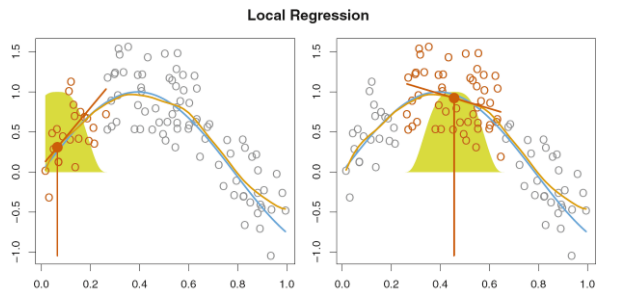
주황색 선은 로컬 회귀로 얻은 함수, 파란색 선은 데이터 자체를 만든 함수입니다. 갈색의 칠해진 점이 해당 영역의 target point고 주변의 빈 갈색 점이 근처 관측치입니다.
여기서 중요한것은 마치 분포와 같이 표시된 노란색 종모양 부분인데요. 이는 해당 영역 내의 각 점에 부가하는 가중치를 나타냅니다. 당연히 target point와 가까울 수록 크고 멀수록 작을 모습을 보이네요.
우선 가중치 함수 $K$를 선택해야 합니다. 또한 선형, 상수 또는 이차 회귀 등 어떤 것을 적합할지 여부를 결정해야합니다.
하지면 역시 제일 중요한 선택 사항은 span(영역)인 $s = k/n$입니다.
◾ 절차
1️⃣ target point $x_0$에 가장 가까운 $x_i$를 가진 훈련 포인트의 분수인 $s = k/n$을 수집합니다.
2️⃣ 이 이웃 중 각 포인트에 가중치 $K_{i0} = K(x_i, x_o)$을 할당(가중치 함수 $K$ 선택)하여 $x_0$에서 가장 멀리 떨어진 포인트는 가중치 0이되고 가장 가까운 포인트는 가장 높은 가중치를 갖도록.(이외 이웃 포인트를 제외한 포인트는 가중치 0)
3️⃣ 위에서 언급한 가중치를 사용하여 $y_i$를 $x_i$에 대한 가중 최소 제곱회귀를 적합하기 위해 $\hat{\beta}_0, \hat{\beta}_1$을 찾는다. 이를 찾기 위해서 아래식을 최소화
$$
\sum_{i=1}^n K_{i0} (y_i - \beta_0 - \beta_1x_i)^2 = \sum_{i=1}^n K(x_i,x_0) (y_i - \beta_0 - \beta_1x_i)^2
$$
4️⃣ $x_0$에서의 적합 값은 아래와 같다.
$$
\hat{f}(x_0) = \hat{\beta}_0 + \hat{\beta}_1 x_0
$$
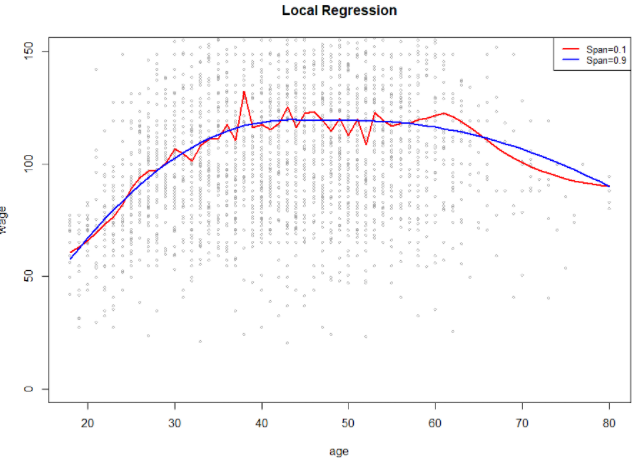
절차를 한번 보았는데 결국 중요한건 $s = k/n$인 span(영역)을 선택하는 것이다. $s$가 클수록 즉, $k$가 클수록 전체 데이터에 대해 적합하고 작을수록 지역적 모형이 만들어진다. span이 작다는건 그만큼 영역을 나누게 되고 이는 overfitting이 될수도 있다는 점을 주의해야 한다.
'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| Smoothing Spline(스무딩 스플라인) (1) | 2023.12.11 |
| 회귀 스플라인(Regression Spline) 그리고 Cubic spline? (1) | 2023.12.11 |
| 다항식 회귀(Polynomial regression) 그리고 계단 함수(Step function) (1) | 2023.12.07 |
📌 로컬 회귀(Local Regression)
로컬 회귀 자체는 스플라인과 유사하지만 영역(region)들이 서로 겹치도록 허용되며, 이들 영역은 부드럽게 연결됩니다.
비모수 회귀 방법 중 하나로, 특히 데이터의 지역적인 패턴을 보고자 할 때 유용합니다. 기본적으로 특정 관측치 주변에서 회귀 모델을 만들어 해당 지역의 패턴을 파악하고, 이를 다른 지역과 겹치게 함으로써 전체 데이터에 대한 부드러운 회귀 모델을 형성합니다.
당연히 데이터가 지역적 특징을 가질 때 유용하고, 스플라인과 같은 전역적인 회귀모델은 전체 데이터에 대한 단일한 함수를 가정하지만, 로컬 회귀는 데이터의 지역적 특성을 놓치지 않고 볼 수 있습니다. 즉! 데이터가 비선형성이 강하고 지역적인 특이성을 파악하고자 할 때 사용합니다.
어떠한 target point ($x_0$) 근처의 관측치 만을 사용하여 함수의 적합을 해나갑니다.(메모리 기반 절차)


주황색 선은 로컬 회귀로 얻은 함수, 파란색 선은 데이터 자체를 만든 함수입니다. 갈색의 칠해진 점이 해당 영역의 target point고 주변의 빈 갈색 점이 근처 관측치입니다.
여기서 중요한것은 마치 분포와 같이 표시된 노란색 종모양 부분인데요. 이는 해당 영역 내의 각 점에 부가하는 가중치를 나타냅니다. 당연히 target point와 가까울 수록 크고 멀수록 작을 모습을 보이네요.
우선 가중치 함수 $K$를 선택해야 합니다. 또한 선형, 상수 또는 이차 회귀 등 어떤 것을 적합할지 여부를 결정해야합니다.
하지면 역시 제일 중요한 선택 사항은 span(영역)인 $s = k/n$입니다.
◾ 절차
1️⃣ target point $x_0$에 가장 가까운 $x_i$를 가진 훈련 포인트의 분수인 $s = k/n$을 수집합니다.
2️⃣ 이 이웃 중 각 포인트에 가중치 $K_{i0} = K(x_i, x_o)$을 할당(가중치 함수 $K$ 선택)하여 $x_0$에서 가장 멀리 떨어진 포인트는 가중치 0이되고 가장 가까운 포인트는 가장 높은 가중치를 갖도록.(이외 이웃 포인트를 제외한 포인트는 가중치 0)
3️⃣ 위에서 언급한 가중치를 사용하여 $y_i$를 $x_i$에 대한 가중 최소 제곱회귀를 적합하기 위해 $\hat{\beta}_0, \hat{\beta}_1$을 찾는다. 이를 찾기 위해서 아래식을 최소화
$$
\sum_{i=1}^n K_{i0} (y_i - \beta_0 - \beta_1x_i)^2 = \sum_{i=1}^n K(x_i,x_0) (y_i - \beta_0 - \beta_1x_i)^2
$$
4️⃣ $x_0$에서의 적합 값은 아래와 같다.
$$
\hat{f}(x_0) = \hat{\beta}_0 + \hat{\beta}_1 x_0
$$
절차를 한번 보았는데 결국 중요한건 $s = k/n$인 span(영역)을 선택하는 것이다. $s$가 클수록 즉, $k$가 클수록 전체 데이터에 대해 적합하고 작을수록 지역적 모형이 만들어진다. span이 작다는건 그만큼 영역을 나누게 되고 이는 overfitting이 될수도 있다는 점을 주의해야 한다.

'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| Smoothing Spline(스무딩 스플라인) (1) | 2023.12.11 |
| 회귀 스플라인(Regression Spline) 그리고 Cubic spline? (1) | 2023.12.11 |
| 다항식 회귀(Polynomial regression) 그리고 계단 함수(Step function) (1) | 2023.12.07 |
