수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 회귀 스플라인(Regression Spline)
polynomial(다항식) and step function(계단 함수) 보다 유연하고 실제로는 이 두 방식의 확장한 버전으로 볼 수 있습니다.
$X$의 범위를 $K$개의 구간으로 나누고(계단 방식) 각 구간안에서 데이터에 대한 다항식 함수(다항 방식)를 적합시킵니다.
그러나 여기서 한 가지. 이런 다항식은 구간의 경계 또는 결속점이라 하는 knots에서 매끄럽게 연결되도록 제약이 가해집니다. 쉽게 말하면 구간의 경계의 끝은 서로 연결되어야 한다는 점입니다.
◾ 분할 다항식(Piecewise Polynomials), 결속점(knots)
분항 다항식과 결속점(knots)가 사용됩니다. 예를 들어 두개의 범위만 봅시다. 하나의 결속점인 $c$와 각각의 범위에 대한 다항식을 아래와 같이 사용합니다.
$$
y_i = \begin{cases}
\beta_{01} + \beta_{11}x_i + \beta_{21}x_i^2 + \beta_{31}x_i^3 + \epsilon_i & \text{for } x_i < c
\\ \beta_{02} + \beta_{12}x_i + \beta_{22}x_i^2 + \beta_{32}x_i^3 + \epsilon_i & \text{for } x_i \geq c
\end{cases}
$$
◾ 제약 조건과 스플라인 그리고 자유도
앞서 knots인 $c$에서 매끄럽게 연결되도록 제약이 가해진다고 하였습니다.
이를 수학적인 설명으로 본다면 연속성, 일차 도함수의 연속성 및 이차 도함수의 연속성이라는 제약을 부과한 것입니다.
쉽게 그림을 통해 살펴보겠습니다.


우선 왼쪽 상단 그림(Piecewise Cubic)은 $Age=50$을 knot로 합니다. 하지만 앞서 제약한 것과 달리 연속적이지 않은 모습을 볼 수 있습니다. 이러한 문제 때문에 앞서 말한 제약을 추가하는 것입니다. 때문에 이러한 제약의 결과가 오른쪽 상단 그림(Continuous Piecewise Cubic)입니다.
그런데 오른쪽 상단의 그림도 매끄럽지 못합니다. $Age=50$ 부분에서 연속이라고는 하나 제약이 더 필요해 보입니다. 이를 위해 두 가지 제약을 더 추가하는 것입니다. 1차, 2차 미분계수가 연속이 되도록 제약을 걸어 결과적으로 왼쪽 아래 그림의 결과가 나오는 것입니다.(Cubic Spline)
여기서 자유도를 살펴보면 오른쪽 상단 그림(Continuous Piecewise Cubic)의 경우 제약이 1개 이므로 자유도는 8(2개의 모형에서 각각 파라미터 4개) - 1(한 가지 제약) =7이 됩니다.
왼쪽 아래(Cubioc Spline)의 경우 8 - 3(세 가지 제약) = 5가 됩니다.
여기서 일반적으로 자유도에 대한 이야기가 있는데 knot의 개수 $K$에서 $+4$를 한 것이 Cubic Spline의 자유도라고 합니다.
그렇다면 오른쪽 아래 그림(Linear Spline)은 뭘까요? 우선 다항식이 아닌 선형식입니다. 때문에 파라미터수와 제약은 knot에서 연속인 점 하나이므로 자유도가 4(2개의 모형에서 각각 파라미터 2개) - 1(한 가지 제약) = 3이 됩니다.
이해가 되셨나요?
◾ Spline 기저식
$K$개의 knots을 갖는 3차 스플라인의 경우 다음과 같이 모델링이 가능하다.
$$
y_i = \beta_0 + \beta_1b_1(x_i) + ... + \beta_{K+3}b_{K+3}(x_i) + \epsilon_i
$$
이러한 다항식을 표현하는 방법에는 여러 가지가 있는데 3차 스플라인을 가장 직접적으로 표현하는 방법 중 하나는 3차 다항식에 대한 기저로 $x, x^2, x^3$을 가지고 시작해서 knots 당 하나의 절단 멱기저 함수(truncated power basis function)를 추가하는 것이다. truncated power basis function은 아래와 같다.
$$
h(x, \xi) = (x-\xi)^3_+ = \begin{cases} (x-\xi)^3 & \text{if } x>\xi \\ 0 & \text{otherwise} \end{cases}
$$
$K$개의 knots를 갖는 데이터 세트에 3차 스플라인을 맞추기 위해, 최소 제곱회귀(least squares regression)를 수행할 수 있습니다. 이때 절편(intercept)과 $K+3$개의 예측 변수가 포함됩니다.(상수를 포함한 $K+4$개의 기저함수)
즉, Cubic Splines에서는 $K+4$개의 계수 추정이 필요합니다. 아까 위에서 Cubic Spline의 자유도는 $K+4$라고 하였죠? 이 때문입니다.
$$
1, x, x^2, x^3, h(x,\xi_1),h(x,\xi_2),...,h(x,\xi_K)
$$
Cubic spline의 한 가지 문제라면 범위 밖의 값들에 대해서는 높은 분산을 가진다는 것입니다.
◾ Knots의 수와 위치
최근엔 소프트웨어가 잘되어있어서 원하는 자유도를 지정한 뒤 소프트웨어가 해당 데이터의 균일한 분위수에 해당하는 knot를 자동으로 배치할 수도 있습니다. 가장 간단한 방법이기도 합니다.(범위에 균일하게 배치하기)
예를 들어 자유도를 7이라고 지정해 주면 cubic spline의 경우 제약식이 3개이기 때문에 7-3=4으로 4개의 knot를 백분위수에 만들어줍니다.
하지만 사실 제일 좋은 점은 cross-validation을 통해 최적의 자유도를 찾는 것이 우선인 것 같습니다. 직접 그래프를 그려보며 확인할 수도 있고요.
◾ Natural cubic spline
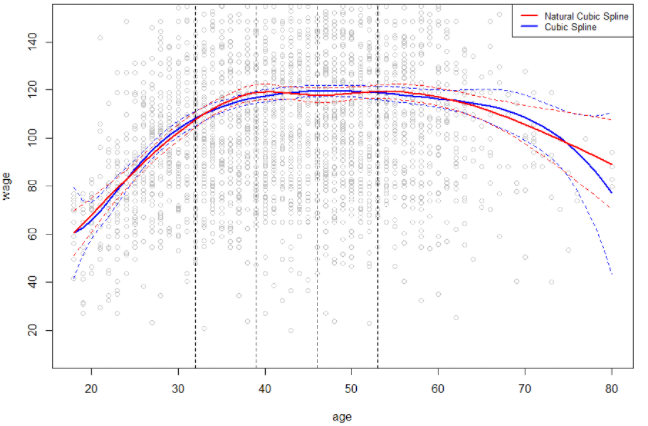
추가적인 경계 제약 조건이 있는 regression spline입니다. $X$값이 knot의 가장 작은 값보다도 더 작거나 가장 큰 값보다도 더 클 때 경계에서 선형이어야 한다는 제약입니다.
이를 통해 knot의 양 끝값에서 더 멀리 떨어진 값들에 대해 좀 더 유연하고 선형성을 유지하는 함수를 생성하게 합니다. 즉, 데이터의 끝 부분 또한 중요하게 볼 수 있다는 것입니다.

$K$개의 knot를 가진 자연 큐빅 스플라인은 다음과 같은 $K$개의 기저 함수로 표현됩니다
$$
N_1(x)=1, N_2(x) = x, N_{k+2}(x) = d_k(x)-d_{K-1}(x)
$$
여기서 $d_k(x)$는
$$
d_k(x) = \dfrac{(x-\xi_k)^3_+ = (x-\xi_K)^3_+}{\xi_K - \xi_k}
$$
'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| 로컬 스플라인(Local Spline) (1) | 2023.12.11 |
| Smoothing Spline(스무딩 스플라인) (1) | 2023.12.11 |
| 다항식 회귀(Polynomial regression) 그리고 계단 함수(Step function) (1) | 2023.12.07 |
