수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 Polynomial regression
선형 모델의 확장 중 하나인 다항 회귀입니다. 매우 쉽습니다!
그냥 원래의 예측 변수를 거듭제곱하여 얻은 예측 변수를 추가하는 것입니다. 예를 들어 그냥 $X$가 아닌 $X, X^2, X^3$와 같은 세 변수를 식에 추가하여 예측 변수로 사용하는 것과 같아요.
이 접근은 선형성 가정이 이루어지지 않았을 때(예측 변수 X와 응답 변수 Y간의 선형성) 데이터에 대한 비선형적인 적합을 제공하는 간단한 접근입니다.
아래와 같이 일반적인 선형 모델을 확장하는 것입니다.
$$
\text{for a quantative response} : y_i = \beta_0 + \beta_1x_i +...+\beta_px_i^p + \epsilon_i
\\ \text{for a binary response} : logit[p(Y=1|x)] = \beta_0 + \beta_1x +...+\beta_px^p
$$
위 식은 일반적인 선형 모델이랑 사실상 다를 게 없죠? 때문에 이 식 또한 최소제곱(least square) 방법을 이용해 추정할 수 있습니다.
실제로 4차 이상인 다항식은 사용하지 않는다고 해요. 3차로도 충분히 예측이 가능할뿐더러 차수가 많아질수록 자원이 많이 들기 때문인 것 같습니다. 또한 차수가 늘어갈수록 overfitting 될 수밖에 없겠죠.
📌 Step function
또 다른 방법으로 step function입니다. 변수의 범위를 $K$개의 구간으로 나누어 각 구간을 구분 짓는 qualitative variable을 생성함으로써 구간마다 상수 함수로 적합시키는 효과를 얻습니다.
추가적인 설명을 해보면 어떤 데이터 $\textbf{x} : x_1,...,x_p$가 있다면 이의 범위를 $c_1,...,c_K$로 나눕니다.
그 각 범위에 해당하는 indicator function(맞으면 1, 틀리면 0)을 생성합니다.
$$
\begin{align}
C_0(x) &= I(x_i<c_0)
\\ C_1(x) &= I(c_0 \leq x_i < c_1)
\\ &...
\\ C_{K-1}(x) &= I(c_{K-1} \leq x_i < c_K)
\\ C_K(x) &= I(c_K \leq x_i)
\end{align}
$$
이를 이용하여 선형식을 확장하면 아래와 같습니다.
$$
y_i = \beta_0 +\beta_1C_1(x_1) + ... + \beta_KC_K(x_i) + \epsilon_i
$$
아래 코드는 3차 다항회귀와 Step function을 이용하여 예측해 보고 그래프를 그리는 코드입니다.(데이터 생성에서 random_state를 지정해주지 않아 다를 수도 있어요.)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.base import BaseEstimator, TransformerMixin
# 무작위 데이터 생성
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 3차 다항 회귀 모델
poly_degree = 3
polyreg = make_pipeline(PolynomialFeatures(degree=poly_degree), LinearRegression())
polyreg.fit(X, y)
# 계단 함수 회귀 모델
class StepFunctionTransformer(BaseEstimator, TransformerMixin):
def __init__(self, num_steps=10):
self.num_steps = num_steps
self.step_size = 5 / num_steps
def fit(self, X, y=None):
return self
def transform(self, X):
return np.floor(X / self.step_size)
stepfunc = make_pipeline(StepFunctionTransformer(), LinearRegression())
stepfunc.fit(X, y)
# 계산 및 출력
mse_poly = mean_squared_error(y, polyreg.predict(X))
rmse_poly = np.sqrt(mse_poly)
r2_poly = r2_score(y, polyreg.predict(X))
mse_stepfunc = mean_squared_error(y, stepfunc.predict(X))
rmse_stepfunc = np.sqrt(mse_stepfunc)
r2_stepfunc = r2_score(y, stepfunc.predict(X))
# 결과 출력
print("3rd Degree Polynomial Regression:")
print(f"RMSE: {rmse_poly}")
print(f"R^2: {r2_poly}")
print("\nStep Function Regression:")
print(f"RMSE: {rmse_stepfunc}")
print(f"R^2: {r2_stepfunc}")
# 그래프 그리기
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_poly = polyreg.predict(X_test)
y_stepfunc = stepfunc.predict(X_test)
plt.figure(figsize=(10, 6))
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_poly, color="cornflowerblue", label="polynomial regression")
plt.plot(X_test, y_stepfunc, color="yellowgreen", label="step function regression")
plt.xlabel("data")
plt.ylabel("target")
plt.title("3rd Degree Polynomial Regression vs Step Function Regression")
plt.legend()
plt.show()3rd Degree Polynomial Regression:
RMSE: 0.1148144617871938
R^2: 0.976857075015689
Step Function Regression:
RMSE: 0.4082208616535508
R^2: 0.7074396619816922

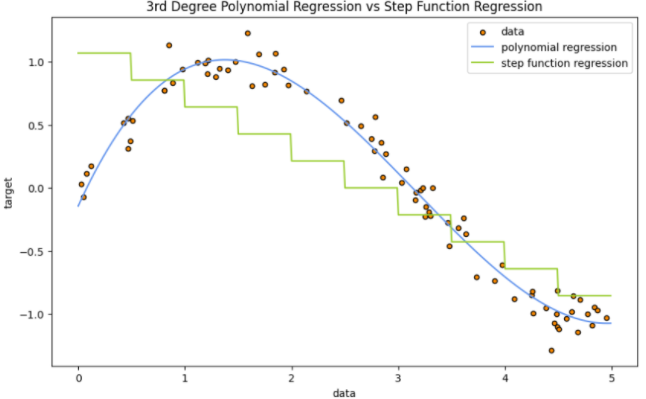
우선 데이터의 점을 보면 선형성을 만족한다고 보기는 어려울 것 같습니다(정확한 검정이 필요! 여기선 예측일 뿐입니다.) 이를 위해 다항회귀와 Step function을 이용하였을 때의 결정력 자체는 다항회귀가 훨씬 높네요. 그래프만 봐도 알 수 있습니다.
여기서 계단을 제 마음대로 임의로 설정해 주었는데 형태를 바꾸어서 올라갔다고 peak에서 내려가는 계단을 이용했다면 결과가 훨씬 좋았을 것 같습니다.
'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| 로컬 스플라인(Local Spline) (1) | 2023.12.11 |
| Smoothing Spline(스무딩 스플라인) (1) | 2023.12.11 |
| 회귀 스플라인(Regression Spline) 그리고 Cubic spline? (1) | 2023.12.11 |
📌 Polynomial regression
선형 모델의 확장 중 하나인 다항 회귀입니다. 매우 쉽습니다!
그냥 원래의 예측 변수를 거듭제곱하여 얻은 예측 변수를 추가하는 것입니다. 예를 들어 그냥 $X$가 아닌 $X, X^2, X^3$와 같은 세 변수를 식에 추가하여 예측 변수로 사용하는 것과 같아요.
이 접근은 선형성 가정이 이루어지지 않았을 때(예측 변수 X와 응답 변수 Y간의 선형성) 데이터에 대한 비선형적인 적합을 제공하는 간단한 접근입니다.
아래와 같이 일반적인 선형 모델을 확장하는 것입니다.
$$
\text{for a quantative response} : y_i = \beta_0 + \beta_1x_i +...+\beta_px_i^p + \epsilon_i
\\ \text{for a binary response} : logit[p(Y=1|x)] = \beta_0 + \beta_1x +...+\beta_px^p
$$
위 식은 일반적인 선형 모델이랑 사실상 다를 게 없죠? 때문에 이 식 또한 최소제곱(least square) 방법을 이용해 추정할 수 있습니다.
실제로 4차 이상인 다항식은 사용하지 않는다고 해요. 3차로도 충분히 예측이 가능할뿐더러 차수가 많아질수록 자원이 많이 들기 때문인 것 같습니다. 또한 차수가 늘어갈수록 overfitting 될 수밖에 없겠죠.
📌 Step function
또 다른 방법으로 step function입니다. 변수의 범위를 $K$개의 구간으로 나누어 각 구간을 구분 짓는 qualitative variable을 생성함으로써 구간마다 상수 함수로 적합시키는 효과를 얻습니다.
추가적인 설명을 해보면 어떤 데이터 $\textbf{x} : x_1,...,x_p$가 있다면 이의 범위를 $c_1,...,c_K$로 나눕니다.
그 각 범위에 해당하는 indicator function(맞으면 1, 틀리면 0)을 생성합니다.
$$
\begin{align}
C_0(x) &= I(x_i<c_0)
\\ C_1(x) &= I(c_0 \leq x_i < c_1)
\\ &...
\\ C_{K-1}(x) &= I(c_{K-1} \leq x_i < c_K)
\\ C_K(x) &= I(c_K \leq x_i)
\end{align}
$$
이를 이용하여 선형식을 확장하면 아래와 같습니다.
$$
y_i = \beta_0 +\beta_1C_1(x_1) + ... + \beta_KC_K(x_i) + \epsilon_i
$$
아래 코드는 3차 다항회귀와 Step function을 이용하여 예측해 보고 그래프를 그리는 코드입니다.(데이터 생성에서 random_state를 지정해주지 않아 다를 수도 있어요.)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.base import BaseEstimator, TransformerMixin
# 무작위 데이터 생성
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 3차 다항 회귀 모델
poly_degree = 3
polyreg = make_pipeline(PolynomialFeatures(degree=poly_degree), LinearRegression())
polyreg.fit(X, y)
# 계단 함수 회귀 모델
class StepFunctionTransformer(BaseEstimator, TransformerMixin):
def __init__(self, num_steps=10):
self.num_steps = num_steps
self.step_size = 5 / num_steps
def fit(self, X, y=None):
return self
def transform(self, X):
return np.floor(X / self.step_size)
stepfunc = make_pipeline(StepFunctionTransformer(), LinearRegression())
stepfunc.fit(X, y)
# 계산 및 출력
mse_poly = mean_squared_error(y, polyreg.predict(X))
rmse_poly = np.sqrt(mse_poly)
r2_poly = r2_score(y, polyreg.predict(X))
mse_stepfunc = mean_squared_error(y, stepfunc.predict(X))
rmse_stepfunc = np.sqrt(mse_stepfunc)
r2_stepfunc = r2_score(y, stepfunc.predict(X))
# 결과 출력
print("3rd Degree Polynomial Regression:")
print(f"RMSE: {rmse_poly}")
print(f"R^2: {r2_poly}")
print("\nStep Function Regression:")
print(f"RMSE: {rmse_stepfunc}")
print(f"R^2: {r2_stepfunc}")
# 그래프 그리기
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_poly = polyreg.predict(X_test)
y_stepfunc = stepfunc.predict(X_test)
plt.figure(figsize=(10, 6))
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_poly, color="cornflowerblue", label="polynomial regression")
plt.plot(X_test, y_stepfunc, color="yellowgreen", label="step function regression")
plt.xlabel("data")
plt.ylabel("target")
plt.title("3rd Degree Polynomial Regression vs Step Function Regression")
plt.legend()
plt.show()3rd Degree Polynomial Regression:
RMSE: 0.1148144617871938
R^2: 0.976857075015689
Step Function Regression:
RMSE: 0.4082208616535508
R^2: 0.7074396619816922


우선 데이터의 점을 보면 선형성을 만족한다고 보기는 어려울 것 같습니다(정확한 검정이 필요! 여기선 예측일 뿐입니다.) 이를 위해 다항회귀와 Step function을 이용하였을 때의 결정력 자체는 다항회귀가 훨씬 높네요. 그래프만 봐도 알 수 있습니다.
여기서 계단을 제 마음대로 임의로 설정해 주었는데 형태를 바꾸어서 올라갔다고 peak에서 내려가는 계단을 이용했다면 결과가 훨씬 좋았을 것 같습니다.
'🌞 Statistics for AI > Regression & Spline' 카테고리의 다른 글
| GAM(Generalized Additive Model) : 일반화 가법 모형 (0) | 2023.12.12 |
|---|---|
| 로컬 스플라인(Local Spline) (1) | 2023.12.11 |
| Smoothing Spline(스무딩 스플라인) (1) | 2023.12.11 |
| 회귀 스플라인(Regression Spline) 그리고 Cubic spline? (1) | 2023.12.11 |
