수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 ROC(Receiver Operating Characteristic) curve analysis
ROC는 우리가 이진 분류 모델의 성능을 파악할 때 사용합니다. 모델의 성능을 시각적으로 확인할 수 있는 통계적 그래픽 요소입니다.
보통 우리가 분류를 할 때 사용하는 결정 임계값은 0.5입니다. 이는 모델이 예측한 확률로 특정 데이터 포인트의 클래스를 결정하는 기준 값입니다.
ROC는 0.5뿐 아닌 다양한 결정 임계값에서 어떻게 작동하는지 성능을 나타냅니다.
ROC 곡선은 다음 두 가지의 주요 지표를 그림으로 나타냅니다.
$$
\text{Sensitivity} = \dfrac{TP}{TP+FN}
\\ \text{1-Specificity} = \dfrac{FP}{FP+TN}
$$
구조를 보시면 아시겠지만 한쪽이 올라가면 한쪽은 내려갈 수밖에 없습니다.
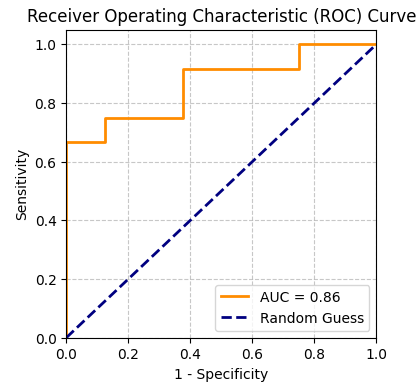
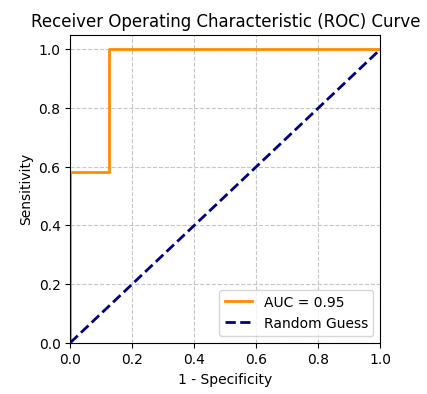
아래 그림을 보면 y축은 Sensitivity, x축은 1 - Specificity로 나타납니다. 주황색 선이 두 번째 그림과 가까운 모습을 할수록 좋은 성능이라고 볼 수 있습니다.
또한 계단처럼 나타나는 것은 결정 임계값과 관련이 있습니다. 결정 임계값은 모델이 데이터 포인트를 양성으로 분류하는 확률의 기준인데, 이 값을 조절하면 당연히 Sensitivity가 변하기 때문에 ROC curve 또한 변화하게 됩니다.


◾ ROC curve 그리기
우리가 데이터 포인트 10개를 가지고 있다고 합시다. 각각의 데이터 포인트에서 양성으로 분류될 확률을 $\hat{p_i}$라고 할 때 아래와 같은 데이터 포인트 표가 있습니다.
본 표에서는 $x_i$의 순서와 확률 값의 순서가 같지만 실제로는 아닐 수 있습니다.
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $x_5$ | $x_6$ | $x_7$ | $x_8$ | $x_9$ | $x_{10}$ | |
| 실제 Class | P | N | P | P | N | P | N | N | P | P |
| $\hat{p}_i$ | 0.9 | 0.7 | 0.6 | 0.58 | 0.5 | 0.42 | 0.38 | 0.33 | 0.2 | 0.1 |
1️⃣ 결정 경계 설정
연구자 본인이 결정 경계를 설정합니다. 여러 가지 결정 임계값을 설정하는 것입니다. 저는 0에서 1까지 0.1의 차이를 기준으로 설정하겠습니다.(가장 좋은 것은 각 확률이 있으니까 이를 기준으로 나누는 것이 좋습니다. 예를들어 $x_7 = 0.38, x_8 = 0.33$확률이니까 그 사이인 0.35를 추가하는 등으로 말이죠)
2️⃣ 분류 진행
각 결정 경계에 맞춰서 모델의 예측 확률인 $\hat{p}_i$와 결정 경계를 비교하여 양성으로 분류되는지 음성으로 분류되는지 확인합니다.
3️⃣ Sensitivity, 1 - Specificity 계산
각 결정경계에서 민감도와 1 - 특이도를 계산합니다.
위 예시로 보았을 때 결정 경계가 0.8일 경우를 보면, $x_1$을 제외한 나머지 모두 음성으로 분류됩니다. 그럼 이때 혼동행렬을 아래와 같아집니다.
| Real Positive | Real Negative | |
|---|---|---|
| Pred Postivie | 1 (TP) | 0 (FP) |
| Pred Negative | 5 (FN) | 4 (TN) |
이때 Sensitivity와 1-Specificity를 계산하면 아래와 같습니다.
$$
\text{Sensitivity} = \dfrac{TP}{TP+FN} = \dfrac{1}{1+5} = 0.16667
\\ \text{1-Specificity} = \dfrac{FP}{FP+TN} = \dfrac{0}{0+4} = 0
$$
이를 통해 $(x,y)$좌표인 (1-Specificity, Sensitivity)를 얻은 겁니다. (0, 0.16667)을 얻은 것이죠.
이처럼 모든 결정 경계에서 계산하여 차근차근 그래프를 그려나갑니다. (0,0)에서 (1,1)로 가도록 그리는 것입니다. 모든 결정 경계에서 (1-Specificity, Sensitivity) 값은 아래와 같습니다.
| 결정 경계 | 1-Specificity | Sensitivity |
|---|---|---|
| 1.0 | 0.00 | 0.00 |
| 0.9 | 0.00 | 0.1667 |
| 0.8 | 0.00 | 0.1667 |
| 0.7 | 0.25 | 0.1667 |
| 0.6 | 0.25 | 0.333 |
| 0.5 | 0.50 | 0.50 |
| 0.4 | 0.50 | 0.6667 |
| 0.3 | 1.00 | 0.6667 |
| 0.2 | 1.00 | 0.833 |
| 0.1 | 1.00 | 1.00 |
| 0.0 | 1.00 | 1.00 |
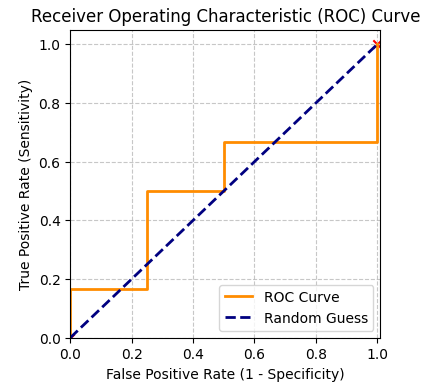

◾ 최적의 결정 경계?
보통 inbalanced data의 경우 결정 경계 0.5에서 정확도가 그리 좋지 못합니다.
그래서 가장 정확도가 좋은 결정경계를 찾아 사용할 수도 있죠. 그럼 이를 어떻게 찾을 까요? 정확도의 식을 봅시다. 아래 식에서 $W$은 전체 샘플을 말하고 $P$는 양성인 모든 샘플, $N$은 음성인 모든 샘플입니다.
$$
\begin{align}
acc &= \dfrac{TP+TN}{W} = \dfrac{TP}{P} \cdot \dfrac{P}{W} + \dfrac{TN}{N} \cdot \dfrac{N}{W}
\\ &= y\dfrac PW + (1-x)\dfrac NW
\\ y &= \dfrac{N/W}{P/W}x + \dfrac{acc-N/W}{P/W}
\end{align}
$$
이렇게 y는 x에 대한 일차함수의 형태를 가지게 됩니다. 여기서 y는 특정 결정 경곗값에서의 정확도를 나타내며 이 x가 해당 결정 경곗값입니다. 따라서 y를 최대로 하는 x를 찾으면 최적의 결정 경계를 찾을 수 있습니다.
실제 curve 그래프를 볼 때, 그래프의 좌상단에 가까운 지점이 가장 적합한 결정 경계라고 볼 수 있습니다.
📌 AUC
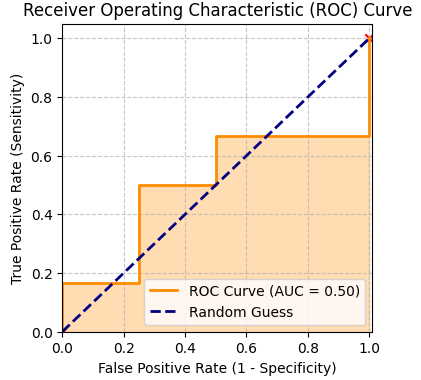
AUC는 ROC curve에서 x축을 밑변으로 하는 넓이를 말합니다. 해당 넓이가 1에 가까울수록 좋은 성능의 모델이라고 할 수 있습니다.
아래는 우리가 예제로 얻은 AUC입니다. 0.5인 것으로 보아 그다지 좋은 성능은 아닙니다.

'🌞 Statistics for AI > Machine learning' 카테고리의 다른 글
| 앙상블(Ensemble) : Stacking(with python) (1) | 2023.12.07 |
|---|---|
| 앙상블(Ensemble) : Voting model(Hard, Soft, Weighted) (1) | 2023.12.07 |
| Cohen's kappa(코헨의 카파) (1) | 2023.12.05 |
| 혼동 행렬(Confusion Matrix) 설명 (1) | 2023.12.05 |
| XGboost with R (1) | 2023.10.15 |
