수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
오늘은 좀 근본적인 이야기를 해볼까 합니다.
우리가 흔히 아는 선형회귀(단순, 다중) 모델들은 Y가 양적 변수인 것을 가정하죠. 하지만 실제로 질적 변수가 필요한 경우가 많습니다.
코로나에 감염이 되었는지(Yes), 되지 않았는지(No) / 범죄자가 유죄인지(guilty), 무죄인지(innocent) 등과 같이 말이죠.
이때 이러한 질적 변수 Y를 예측하는 것을 분류한다고 합니다. 이 Y를 특정 범주 혹은 class로 할당하는 것이기 때문이죠.
그런데 보통 분류를 위해 회귀를 사용하지는 않습니다. 질적 변수를 1, 0 등으로 두어 1과 가깝다면 A, 0과 가깝다면 B로 분류할 수도 있지 않을까요?
왜? 선형회귀를 사용하지 않을까요?
예를 들어봅시다. 우리가 코로나에 영성인지 음성인지 본다면 Y를 이렇게 놓을 수 있겠죠.

이에 대한 설명 변수 X1, X2, ... , Xp를 이용해 Y를 예측하는 회귀모델을 적합하는데, 최소제곱법을 사용할 수 있습니다.
하지만 이런식의 가정은 결과값에 순서가 있다는 것을 의미합니다. 양성이 음성보다 높은 값인가요? 그저 감염이 되었다, 아니다의 의미일 뿐입니다.
물론 이진 반응변수를 예측할 때에 사용할 수 있긴 합니다만.. 시각적으로 그래프를 그려보면
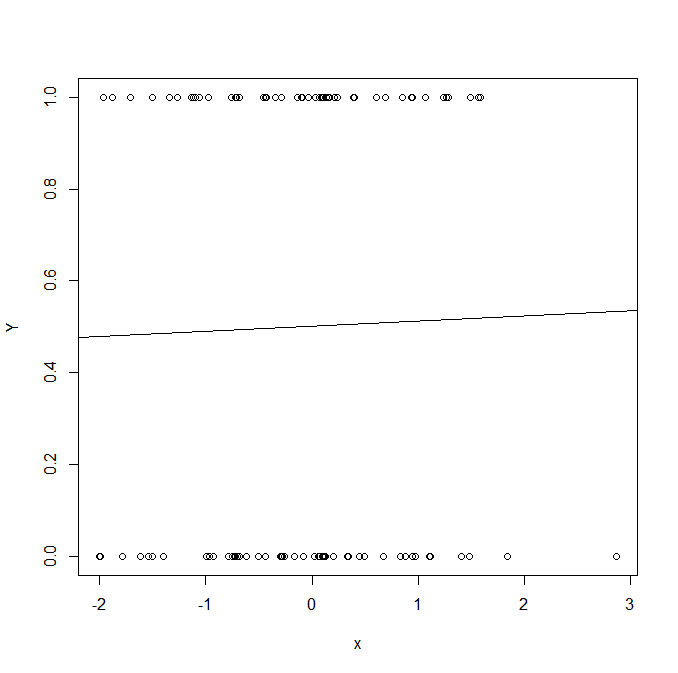
굉장히 극단적인 예시기는 하나.. 그래프만 보아도 회귀식이 큰 의미가 있을 것 같지는 않습니다. 심지어 x가 점점더 음의 값으로 갈수록, 양의 값으로 갈수록 Y값인 0과 1에서 더욱 멀어집니다.
값 Y가 0~1사이의 값이 아닌 5, 혹은 10과 같이 나온다면 어떻게 판단해야 할까요?
또한 이진 변수가 아닌 수준이 3개 이상 넘어가면 더욱 복잡해지기 때문에 우리는 회귀가 아닌 분류를 사용합니다.
'📊 Statistics for Basic > 기초 통계' 카테고리의 다른 글
| 가능도(Likelihood) vs 확률(Probability) (1) | 2024.04.23 |
|---|---|
| 확률 변수(이산과 연속) (0) | 2023.11.15 |
| 불편추정량. n-1로 나누는 이유 (0) | 2023.10.03 |
| 중심극한정리 (0) | 2023.10.03 |
| 확률변수의 분산과 상관계수 (0) | 2023.10.03 |
오늘은 좀 근본적인 이야기를 해볼까 합니다.
우리가 흔히 아는 선형회귀(단순, 다중) 모델들은 Y가 양적 변수인 것을 가정하죠. 하지만 실제로 질적 변수가 필요한 경우가 많습니다.
코로나에 감염이 되었는지(Yes), 되지 않았는지(No) / 범죄자가 유죄인지(guilty), 무죄인지(innocent) 등과 같이 말이죠.
이때 이러한 질적 변수 Y를 예측하는 것을 분류한다고 합니다. 이 Y를 특정 범주 혹은 class로 할당하는 것이기 때문이죠.
그런데 보통 분류를 위해 회귀를 사용하지는 않습니다. 질적 변수를 1, 0 등으로 두어 1과 가깝다면 A, 0과 가깝다면 B로 분류할 수도 있지 않을까요?
왜? 선형회귀를 사용하지 않을까요?
예를 들어봅시다. 우리가 코로나에 영성인지 음성인지 본다면 Y를 이렇게 놓을 수 있겠죠.

이에 대한 설명 변수 X1, X2, ... , Xp를 이용해 Y를 예측하는 회귀모델을 적합하는데, 최소제곱법을 사용할 수 있습니다.
하지만 이런식의 가정은 결과값에 순서가 있다는 것을 의미합니다. 양성이 음성보다 높은 값인가요? 그저 감염이 되었다, 아니다의 의미일 뿐입니다.
물론 이진 반응변수를 예측할 때에 사용할 수 있긴 합니다만.. 시각적으로 그래프를 그려보면

굉장히 극단적인 예시기는 하나.. 그래프만 보아도 회귀식이 큰 의미가 있을 것 같지는 않습니다. 심지어 x가 점점더 음의 값으로 갈수록, 양의 값으로 갈수록 Y값인 0과 1에서 더욱 멀어집니다.
값 Y가 0~1사이의 값이 아닌 5, 혹은 10과 같이 나온다면 어떻게 판단해야 할까요?
또한 이진 변수가 아닌 수준이 3개 이상 넘어가면 더욱 복잡해지기 때문에 우리는 회귀가 아닌 분류를 사용합니다.
'📊 Statistics for Basic > 기초 통계' 카테고리의 다른 글
| 가능도(Likelihood) vs 확률(Probability) (1) | 2024.04.23 |
|---|---|
| 확률 변수(이산과 연속) (0) | 2023.11.15 |
| 불편추정량. n-1로 나누는 이유 (0) | 2023.10.03 |
| 중심극한정리 (0) | 2023.10.03 |
| 확률변수의 분산과 상관계수 (0) | 2023.10.03 |