수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 로지스틱 회귀
로지스틱 회귀에 대한 간단한 식의 설명. 계수 구하는 방법과 같은 과정은 후에 다뤄보도록 하자.
일반적인 선형회귀에 대하 아실것이라 가정하고 로지스틱 회귀를 한번 봅시다. 기본적으로 독립 변수들의 선형 결합으로 표현하는 방정식을 통해 종속 변수를 표현하는 것을 유사 합니다.
가장 큰 차이는 종속 변수의 차이입니다. 선형 회귀의 경우 연속 변수이지만 로지스틱 회귀의 경우 종속 변수가 범주형 변수일 경우 사용하게 됩니다. 그러니 이름에 회귀!가 있지만? 일종의 분류 기법으로 사용하는 것입니다.
정말 간단한 모델로 우리가 어떠한 분류 문제를 다룰 때 제일 먼저 사용해보아야할 모델이기도 합니다. 간단한 모델로 충분한 성능이 나온다면 굳이 어렵고 복잡한 모델을 사용할 필요가 적겠죠??
회귀의 결과값은 아래와 같이 항상 [0,1]로 제한되어 있습니다. 이미 포스팅 했던 분류에 회귀를 사용하지 않는 이유를 보시면 이해가 편할 것입니다. (링크 : 분류에 선형회귀를 사용하지 않는 이유)

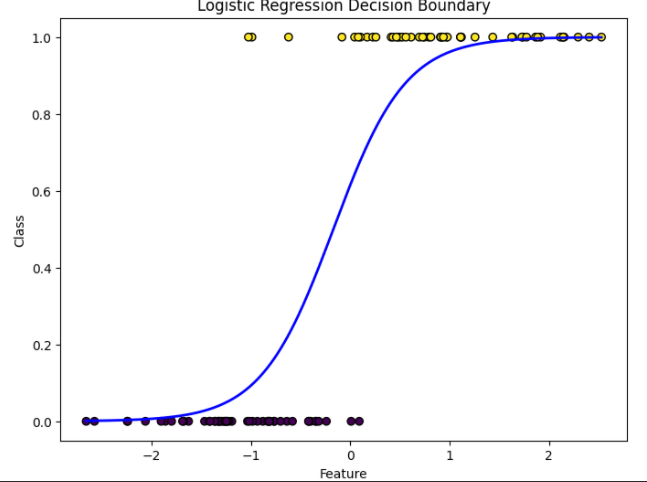
로지스틱을 이용하면 더이상 값이 0 미만, 1 초과로 이어지지 않기 때문에 분류에 사용할 수 있는 것입니다.
◼️ odds, logit
$Y= \text{1 or 0}$으로 봅시다. 이에 대한 로지스틱 회귀는 reponse가 특정 범주에 속할 확률 $P(Y=1|X)$를 모델링합니다.
성공확률(여기선 1을 성공으로 보겠습니다.)이 실패 확률에 비해 얼마나 높은가? 를 나타내는 odds(오즈) 식은 아래와 같습니다.
$$
odds = \dfrac{P(Y=1|X)}{P(Y=0|X)} = \dfrac{P(Y=1|X)}{1-P(Y=1|X)}
$$
이 odds에 로그를 취하여 값의 범위를 [0, 1] 로 제한하는 것이 아이디어 입니다. 이 값이 logit입니다.
$$
logit = \log(odds) = \log \left( \dfrac{P(Y=1|X)}{1-P(Y=1|X)} \right)
$$
이를 회귀식으로 표현하여 아래와 같은 로지스틱 회귀식을 만들고 각 베타값을 찾습니다.
$$
\log \left( \dfrac{P(Y=1|X)}{1-P(Y=1|X)} \right) = \beta_0 + \beta_1 X
$$
이 때 $p(Y=1|X)$를 간단하게 $p(X)$로 표현하고 $p(X)$에 대해 정의하면 아래와 같습니다.
$$
P(Y=1|X) = p(X) = \dfrac{\exp(\beta_0 + \beta_1 X)}{1 + \exp(\beta_0 + \beta_1 X)}
\ P(Y=0|X) = 1-p(X) = \dfrac{1}{1 + \exp(\beta_0 + \beta_1 X)}
$$
◼️ 로지스틱 회귀에 대한 해석
선형회귀에서 $\beta_0$은 intercept이고 $\beta_1$은 기울기 인데 로지스틱 회귀에서 $\beta_1$은 무엇을 뜻할까? (당연 $\beta_0$은 X가 0일 때의 값일 것이다.)
$X+1$에서의 로짓에서 $X$에서의 로짓을 빼서 $\beta_1$을 확인하면 아래와 같습니다.
$$
\log\dfrac{p(X+1)}{1-p(X+1)} - \log\dfrac{p(X)}{1-p(X)} = \beta_0+\beta_1(X+1) - (\beta_0 + \beta_1X)
$$
$$
\log \dfrac{p(X+1)(1-p(X))}{(1-p(X+1))p(X)} = \beta_1
$$
위 식으로 보았을 때 이는 클래스 $Y=1$의 로짓($\log(odds)$)의 $X+1$과 $X$간의 비율입니다. 쉽게 설명하면 1이 더해졌을 때 증가하는 odds의 비율을 알 수 있다는 것입니다.
예를 들어 $\beta_1 = 0.4$ 라면 $odds$를 구하기 위해 exponential을 취하면 $\exp(0.4) \approx 1.5$가 됩니다. 이는 $X+1$에서의 $odds$가 $X$에서의 $odds$보다 1.5배 라는 것이겠죠.
📌다중 로지스틱 회귀(Multinomial logistic regression)
단순히 0 or 1, Yes or No의 2가지 클래스가 아닌 여러 클래스가 있을 경우에는 로짓 모델을 아래와 같이 표현할 수 있습니다. 행렬로 표현이 가능합니다.
$$
\begin{align}
\log \dfrac{P(Y=i|X_1=x_1,...,X_p=x_p)}{P(Y=K|X_1=x_1,...,X_p=x_p)} &= \beta_{i0} + \beta_{i1}x_1 +...+ \beta_{ip}x_p \ \ (i = 1,..., K-1) \\ &= \pmb{\beta_i}^T \textbf{x}
\end{align}
$$
이를 통해 $\textbf{X} = \textbf{x}$가 주어졌을 때 $Y=i$의 조건부 확률을 구하면 아래와 같습니다.
$$
P(Y=i|\textbf{X} = \textbf{x}) = \dfrac{\exp(\pmb{\beta_i}^T \textbf{x})}{1+ \Sigma_{m=1}^{K-1} \exp(\pmb{\beta_m}^T \textbf{x})}
\\ P(Y=K|\textbf{X} = \textbf{x}) = \dfrac{1}{1+ \Sigma_{m=1}^{K-1} \exp(\pmb{\beta_m}^T \textbf{x})}
$$
좀 더 복잡해 보일뿐, 기본적인 원리와 구조는 이진 로지스틱 회귀와 유사한걸 알 수 있습니다.
'🌞 Statistics for AI > Classification' 카테고리의 다른 글
| KNN(K-최근접 이웃) 간단한 설명 (1) | 2023.12.05 |
|---|---|
| 베이즈 분류의 사전확률 추정 (1) | 2023.12.05 |
| 나이브 베이즈 분류(독립성 가정의 중요성?) (1) | 2023.12.03 |
| LDA, QDA 간단한 차이와 방정식 (1) | 2023.12.03 |
| 베이즈 분류와 ECM, TPM, Bayes error rate (2) | 2023.11.29 |
