수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 KNN
KNN의 full name은 K Nearest Neighbors입니다. K의 가까운 이웃이라는 뜻으로 특정 포인트의 가까운 점들의 label 값에 따라 해당 포인트의 label을 분류하게 됩니다.
아래 그림처럼 별을 특정 데이터 포인트라고 하였을 때, k에 따라 다른 label로 분류가 바뀔 수 있습니다.
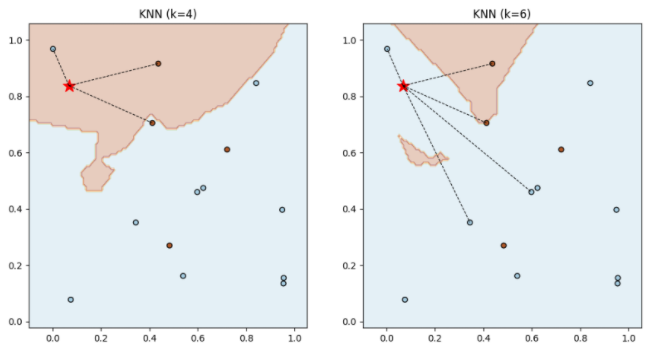
왼쪽 그림의 경우 k=4로 갈색 label이 더 많고, 오른쪽 그림의 경우 k=6으로 파란 label이 더많게 됩니다.

이론적으로는 베이즈 분류기를 사용하여 질적 응답에 대해 예측하는 것입니다. (베이즈 분류 : 링크)
앞서 베이즈 분류를 보고 오셨다면.. 실제 우리는 $P(Y=j|\textbf{X})$인 사전 분포를 모르기 때문에 특정 분포에 대한 가정이 없다면 베이즈 분류기를 구성하는 것이 불가능 합니다.
이를 해결하기 위한 방법중 하나로 KNN(K-최근접 이웃)이라는 비모수적인 방법을 사용하는 것입니다.
두 벡터 사이의 거리 $d(\textbf{x}_1,\textbf{x}_2)$를 이용합니다. 이 때 거리는 보통 유클리디안 거리를 사용하고, 외에도 다른 거리척도를 사용할 수도 있습니다.
우리가 어떤 양의 정수인 $K$를 설정했을 때, KNN 분류기는 우선 test 데이터 $\textbf{x}_0$에 가장 가까운 train 데이터의 $K$개 점을 식별합니다. 이를 $N_k(\textbf{x}_0)$라고 합시다.
그 다음 클래스 $j$에 대한 조건부 확률을 추정합니다. $N_0$에 속하는 점 중에서 응답 값이 $j$인 점의 비율로 나타냅니다. 아래와 같아요
$$
\hat{P}(Y=j|\textbf{X}=\textbf{x}_0) =
\dfrac1K \sum{\textbf{x}_i \in N_K(\textbf{x}_0)} I(y_i=j)
$$
후, 베이즈 규칙을 적용하여 test 데이터 $\textbf{x}_0$을 가장 큰 확률을 가진 클래스로 분류합니다. 말이 어렵지 위 식에서 각 클래스에 할당 될 확률이 가장 큰 값에 할당한다는 이야기 입니다.
아래는 간단한 예제 데이터로 하는 KNN입니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
# 비선형 결정 경계를 가지는 가상의 데이터 생성
np.random.seed(42)
X = np.random.rand(100, 2) * 2 - 1 # [-1, 1] 범위의 무작위 점 생성
y = (X[:, 0]**2 + X[:, 1]**2 > 0.6).astype(int) # 원형 결정 경계 생성
# 데이터를 학습 세트와 테스트 세트로 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# KNN 모델 정의 (여기서는 k=5을 사용)
knn_model = KNeighborsClassifier(n_neighbors=5)
# KNN 모델 학습
knn_model.fit(X_train, y_train)
# 테스트 세트에 대한 예측
y_pred = knn_model.predict(X_test)
# 정확도 계산
accuracy = accuracy_score(y_test, y_pred)
# 그래프로 시각화
plt.figure(figsize=(10, 6))
# 학습 데이터와 테스트 데이터의 산점도
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Paired, edgecolor='k', s=50, label='Train Data')
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=plt.cm.Paired, marker='^', edgecolor='k', s=100, label='Test Data')
# 결정 경계 표시
h = .02 # 메쉬 그리드에서의 단계 크기
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = knn_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.3, levels=[-0.5, 0.5, 1.5])
plt.title(f'KNN Classifier with Boundary(K=5)\nAccuracy: {accuracy:.2f}')
plt.legend()
plt.show()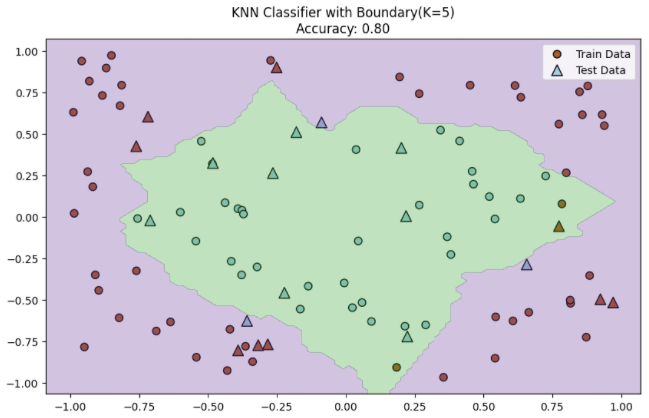
'🌞 Statistics for AI > Classification' 카테고리의 다른 글
| 베이즈 분류의 사전확률 추정 (1) | 2023.12.05 |
|---|---|
| 로지스틱 회귀(+ 다중 로지스틱 회귀)의 간단한 설명 (0) | 2023.12.03 |
| 나이브 베이즈 분류(독립성 가정의 중요성?) (1) | 2023.12.03 |
| LDA, QDA 간단한 차이와 방정식 (0) | 2023.12.03 |
| 베이즈 분류와 ECM, TPM, Bayes error rate (1) | 2023.11.29 |
📌 KNN
KNN의 full name은 K Nearest Neighbors입니다. K의 가까운 이웃이라는 뜻으로 특정 포인트의 가까운 점들의 label 값에 따라 해당 포인트의 label을 분류하게 됩니다.
아래 그림처럼 별을 특정 데이터 포인트라고 하였을 때, k에 따라 다른 label로 분류가 바뀔 수 있습니다.

왼쪽 그림의 경우 k=4로 갈색 label이 더 많고, 오른쪽 그림의 경우 k=6으로 파란 label이 더많게 됩니다.

이론적으로는 베이즈 분류기를 사용하여 질적 응답에 대해 예측하는 것입니다. (베이즈 분류 : 링크)
앞서 베이즈 분류를 보고 오셨다면.. 실제 우리는 P(Y=j|X)인 사전 분포를 모르기 때문에 특정 분포에 대한 가정이 없다면 베이즈 분류기를 구성하는 것이 불가능 합니다.
이를 해결하기 위한 방법중 하나로 KNN(K-최근접 이웃)이라는 비모수적인 방법을 사용하는 것입니다.
두 벡터 사이의 거리 d(x1,x2)를 이용합니다. 이 때 거리는 보통 유클리디안 거리를 사용하고, 외에도 다른 거리척도를 사용할 수도 있습니다.
우리가 어떤 양의 정수인 K를 설정했을 때, KNN 분류기는 우선 test 데이터 x0에 가장 가까운 train 데이터의 K개 점을 식별합니다. 이를 Nk(x0)라고 합시다.
그 다음 클래스 j에 대한 조건부 확률을 추정합니다. N0에 속하는 점 중에서 응답 값이 j인 점의 비율로 나타냅니다. 아래와 같아요
ˆP(Y=j|X=x0)=1K∑xi∈NK(x0)I(yi=j)
후, 베이즈 규칙을 적용하여 test 데이터 x0을 가장 큰 확률을 가진 클래스로 분류합니다. 말이 어렵지 위 식에서 각 클래스에 할당 될 확률이 가장 큰 값에 할당한다는 이야기 입니다.
아래는 간단한 예제 데이터로 하는 KNN입니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
# 비선형 결정 경계를 가지는 가상의 데이터 생성
np.random.seed(42)
X = np.random.rand(100, 2) * 2 - 1 # [-1, 1] 범위의 무작위 점 생성
y = (X[:, 0]**2 + X[:, 1]**2 > 0.6).astype(int) # 원형 결정 경계 생성
# 데이터를 학습 세트와 테스트 세트로 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# KNN 모델 정의 (여기서는 k=5을 사용)
knn_model = KNeighborsClassifier(n_neighbors=5)
# KNN 모델 학습
knn_model.fit(X_train, y_train)
# 테스트 세트에 대한 예측
y_pred = knn_model.predict(X_test)
# 정확도 계산
accuracy = accuracy_score(y_test, y_pred)
# 그래프로 시각화
plt.figure(figsize=(10, 6))
# 학습 데이터와 테스트 데이터의 산점도
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.Paired, edgecolor='k', s=50, label='Train Data')
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=plt.cm.Paired, marker='^', edgecolor='k', s=100, label='Test Data')
# 결정 경계 표시
h = .02 # 메쉬 그리드에서의 단계 크기
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = knn_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.3, levels=[-0.5, 0.5, 1.5])
plt.title(f'KNN Classifier with Boundary(K=5)\nAccuracy: {accuracy:.2f}')
plt.legend()
plt.show()
'🌞 Statistics for AI > Classification' 카테고리의 다른 글
| 베이즈 분류의 사전확률 추정 (1) | 2023.12.05 |
|---|---|
| 로지스틱 회귀(+ 다중 로지스틱 회귀)의 간단한 설명 (0) | 2023.12.03 |
| 나이브 베이즈 분류(독립성 가정의 중요성?) (1) | 2023.12.03 |
| LDA, QDA 간단한 차이와 방정식 (0) | 2023.12.03 |
| 베이즈 분류와 ECM, TPM, Bayes error rate (1) | 2023.11.29 |
