수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
오늘은 저번 확률에 이어서 표본 평균의 분포를 알아보려고 합니다.
표본도 알고 평균도 알고 표본의 평균도 아는데 통계에 있어서 왜 표본 평균의 분포가 중요한 것일까요??
우리는 표본을 통해 모집단을 일반화 합니다. 하지만 의문점은 과연 표본이 모집단을 대표할만한 대표성을 가지고 있느냐가 문제겠지요. 이에 따라서 우리는 어떠한 가정이 필요합니다. 이러한 가정들을 알기 위해서 표본 평균의 분포를 알아보는 것입니다.
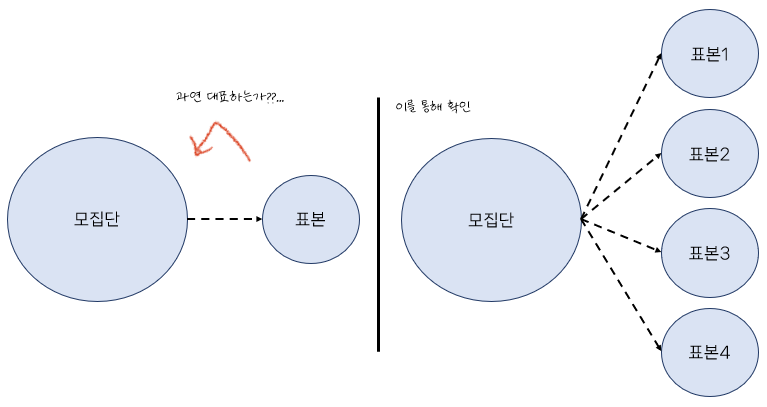
살펴볼 가정들이 존재하기 때문에 우리가 모은 표본을 통해 연구가 가능한 것입니다. 이러한 가정이 없다면 '표본이 결국은 모집단이랑 다른거 아니에요?'라는 질문에 답변할 수 없게 됩니다. 실제로 많은 연구들에서 재현성의 문제가 있다고 연구 결과도 있는 만큼 표본의 중요성은 여러번 강조됩니다.
📌 표본 평균의 분포
아무리 모집단을 대표한다고 하더라도, 이에 상응하는 모수간에는 차이가 존재할 것입니다. 또한, 모집단에서 매번 표본을 표집할 때 동일한 표본을 얻지 못하겠지요. 때문에 우리는 표본 평균에 대한 개념을 알아야 합니다.
- 표본 평균의 분포 : 모집단으로 부터 얻을 수 있는 모든 가능한 특정 크기(n)의 무작위 표본들에 대해 구한 표본 평균들의 분포
말이 어렵겠지만, 쉽게 설명하면 모집단으로 부터 여러 표본들을 뽑고, 이 표본들의 평균값이 그리는 분포라고 볼 수 있습니다.
◼️ 표본 평균 분포의 특징
표본 평균 분포의 특징이 있는데요. 이 특징이 매우 중요합니다.
1. 표본 평균들은 모평균 주위에 모여있을 것이다.(표본들은 모집단과 동일하지는 않지만 모집단을 대표한다.)
2. 표본 평균들은 정규 분포 모양으로 분포할 것이다.
3. 일반적으로 표본 크기가 커질수록 표본 평균들은 모평균에 가까워질것이다.
그럼 이 특징과 가정들을 하나하나 살펴보겠습니다.
먼저 1번과 2번을 한번 확인해 보죠. 경험적인 자료를 통해 확인해보겠습니다.
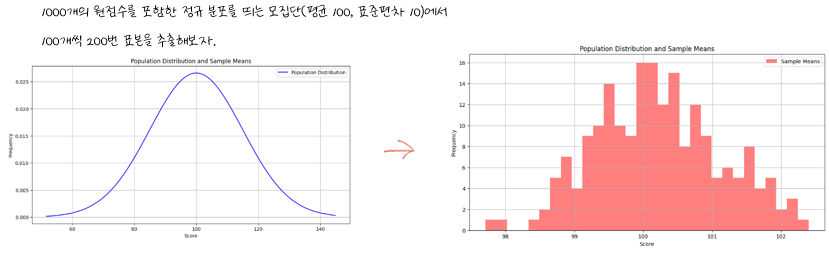
특정 모집단을 만들고, 이 모집단에서 100개씩 200번 표본을 추출해봅시다.
그렇다면 아래 그림과 같이 1. 표본 평균들은 모평균인 100 주위에 모여있으며 2. 표본 평균들은 정규 분포 모양으로 분포하게 됩니다.
이렇게 경험적인 실험으로 1번과 2번을 충족한다는 것을 보았는데요, 경험적인 결과로만 이야기할 수는 없겠죠.
사회적인 약속을 해야합니다. 이 중 하나가 우리가 흔히 듣는 중심 극한 정리 입니다.
✔︎ 중심 극한 정리(Central limit Theorem)
: 평균이 $\mu$이고 표준편차가 $\sigma$인 임의의 모집단에 대해, 표본 크기가 n 표본 평균은 평균이 $\mu$, 표준편차가 $\dfrac{\sigma}{\sqrt{n}}$인 분포를 따르고, n이 무한대에 가까워질수록 정규 분포에 근사한다.
이렇게 중심 극한 정리에 1번과 2번 모두 포함되는 것입니다. 보통 n=30에 도달하면 표본 평균의 분포는 거의 완벽한 정규 분포가 된다고 보고 있습니다.
이어서 3번을 확인해보겠습니다. 표본의 크기를 키워서 표본 평균들을 확인해봅시다.
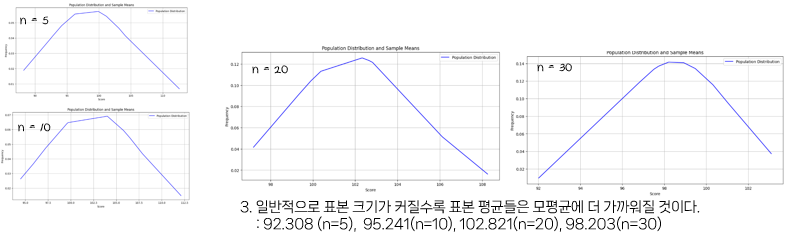
위와 같이 표본의 크기를 5, 10, 20, 30으로 키워갈수록 모평균에 가까워지는 것을 확인할 수 있습니다.
이 또한 사회적 약속을 해야겠지요.
✔︎ 큰 수의 법칙(law of large number)
: 표본 크기(n)가 증가할수록 표본 평균이 모평균에 가까울 가능성이 높다는 것을 말한다.
✔︎ n이 30 이상이어도 정규성을 만족하지 않는다면..?
당연히 n이 30인 경우, 더 나아가서 100, 1000을 넘어선 경우에도 정규성 가정을 만족하지 못할 수도 있습니다.
특히 사회과학 분야에서 흔히 나타날 수 있지요.
먼저, 우리는 n > 30일 경우 정규 분포를 따를 것이라고 약속하였습니다. 때문에, 모수적 통계 방법론을 사용할 수 있습니다. 하지만, 이는 분명 문제가 될 수 있습니다. 가정에 따랐을 뿐 실제 데이터는 그렇지 않기 때문에요.
이러한 이유로 AI가 더욱 발전하기도 했습니다. 우리 세상에 존재하는 많은 데이터들이 정규분포를 따르지 않기 때문입니다. 경우에 따라 다르겠으나. 되도록이면 비모수적 통계 방법을 사용하는 것이 좋을 것 같습니다.
이렇게 표본 평균들의 분포를 통해 중심 극한 정리, 큰 수의 법칙을 알아보았습니다. 전통적인 통계 프레임에서 이들은 중요한 개념이기 때문에 꼭 알아두었으면 좋겠습니다.
'📊 Statistics for Basic > 기초 통계' 카테고리의 다른 글
| 짧은 기초 통 계 7 : 분산 분석(ANOVA) (0) | 2024.08.01 |
|---|---|
| 짧은 기초 통계 6 : 가설 검정, t-test(t 검정) (2) | 2024.07.10 |
| 짧은 기초 통계 4 : z-score(z 점수)와 확률 (1) | 2024.06.26 |
| 짧은 기초 통계 3 : 변산성, 불편 추정량(제약식과 자유도) (1) | 2024.06.16 |
| 짧은 기초 통계 2 : 중심 경향값과 편포(+ 로그/제곱근 변환) (0) | 2024.06.15 |
오늘은 저번 확률에 이어서 표본 평균의 분포를 알아보려고 합니다.
표본도 알고 평균도 알고 표본의 평균도 아는데 통계에 있어서 왜 표본 평균의 분포가 중요한 것일까요??
우리는 표본을 통해 모집단을 일반화 합니다. 하지만 의문점은 과연 표본이 모집단을 대표할만한 대표성을 가지고 있느냐가 문제겠지요. 이에 따라서 우리는 어떠한 가정이 필요합니다. 이러한 가정들을 알기 위해서 표본 평균의 분포를 알아보는 것입니다.

살펴볼 가정들이 존재하기 때문에 우리가 모은 표본을 통해 연구가 가능한 것입니다. 이러한 가정이 없다면 '표본이 결국은 모집단이랑 다른거 아니에요?'라는 질문에 답변할 수 없게 됩니다. 실제로 많은 연구들에서 재현성의 문제가 있다고 연구 결과도 있는 만큼 표본의 중요성은 여러번 강조됩니다.
📌 표본 평균의 분포
아무리 모집단을 대표한다고 하더라도, 이에 상응하는 모수간에는 차이가 존재할 것입니다. 또한, 모집단에서 매번 표본을 표집할 때 동일한 표본을 얻지 못하겠지요. 때문에 우리는 표본 평균에 대한 개념을 알아야 합니다.
- 표본 평균의 분포 : 모집단으로 부터 얻을 수 있는 모든 가능한 특정 크기(n)의 무작위 표본들에 대해 구한 표본 평균들의 분포
말이 어렵겠지만, 쉽게 설명하면 모집단으로 부터 여러 표본들을 뽑고, 이 표본들의 평균값이 그리는 분포라고 볼 수 있습니다.
◼️ 표본 평균 분포의 특징
표본 평균 분포의 특징이 있는데요. 이 특징이 매우 중요합니다.
1. 표본 평균들은 모평균 주위에 모여있을 것이다.(표본들은 모집단과 동일하지는 않지만 모집단을 대표한다.)
2. 표본 평균들은 정규 분포 모양으로 분포할 것이다.
3. 일반적으로 표본 크기가 커질수록 표본 평균들은 모평균에 가까워질것이다.
그럼 이 특징과 가정들을 하나하나 살펴보겠습니다.
먼저 1번과 2번을 한번 확인해 보죠. 경험적인 자료를 통해 확인해보겠습니다.
특정 모집단을 만들고, 이 모집단에서 100개씩 200번 표본을 추출해봅시다.
그렇다면 아래 그림과 같이 1. 표본 평균들은 모평균인 100 주위에 모여있으며 2. 표본 평균들은 정규 분포 모양으로 분포하게 됩니다.

이렇게 경험적인 실험으로 1번과 2번을 충족한다는 것을 보았는데요, 경험적인 결과로만 이야기할 수는 없겠죠.
사회적인 약속을 해야합니다. 이 중 하나가 우리가 흔히 듣는 중심 극한 정리 입니다.
✔︎ 중심 극한 정리(Central limit Theorem)
: 평균이 μ이고 표준편차가 σ인 임의의 모집단에 대해, 표본 크기가 n 표본 평균은 평균이 μ, 표준편차가 σ√n인 분포를 따르고, n이 무한대에 가까워질수록 정규 분포에 근사한다.
이렇게 중심 극한 정리에 1번과 2번 모두 포함되는 것입니다. 보통 n=30에 도달하면 표본 평균의 분포는 거의 완벽한 정규 분포가 된다고 보고 있습니다.
이어서 3번을 확인해보겠습니다. 표본의 크기를 키워서 표본 평균들을 확인해봅시다.

위와 같이 표본의 크기를 5, 10, 20, 30으로 키워갈수록 모평균에 가까워지는 것을 확인할 수 있습니다.
이 또한 사회적 약속을 해야겠지요.
✔︎ 큰 수의 법칙(law of large number)
: 표본 크기(n)가 증가할수록 표본 평균이 모평균에 가까울 가능성이 높다는 것을 말한다.
✔︎ n이 30 이상이어도 정규성을 만족하지 않는다면..?
당연히 n이 30인 경우, 더 나아가서 100, 1000을 넘어선 경우에도 정규성 가정을 만족하지 못할 수도 있습니다.
특히 사회과학 분야에서 흔히 나타날 수 있지요.
먼저, 우리는 n > 30일 경우 정규 분포를 따를 것이라고 약속하였습니다. 때문에, 모수적 통계 방법론을 사용할 수 있습니다. 하지만, 이는 분명 문제가 될 수 있습니다. 가정에 따랐을 뿐 실제 데이터는 그렇지 않기 때문에요.
이러한 이유로 AI가 더욱 발전하기도 했습니다. 우리 세상에 존재하는 많은 데이터들이 정규분포를 따르지 않기 때문입니다. 경우에 따라 다르겠으나. 되도록이면 비모수적 통계 방법을 사용하는 것이 좋을 것 같습니다.
이렇게 표본 평균들의 분포를 통해 중심 극한 정리, 큰 수의 법칙을 알아보았습니다. 전통적인 통계 프레임에서 이들은 중요한 개념이기 때문에 꼭 알아두었으면 좋겠습니다.
'📊 Statistics for Basic > 기초 통계' 카테고리의 다른 글
| 짧은 기초 통 계 7 : 분산 분석(ANOVA) (0) | 2024.08.01 |
|---|---|
| 짧은 기초 통계 6 : 가설 검정, t-test(t 검정) (2) | 2024.07.10 |
| 짧은 기초 통계 4 : z-score(z 점수)와 확률 (1) | 2024.06.26 |
| 짧은 기초 통계 3 : 변산성, 불편 추정량(제약식과 자유도) (1) | 2024.06.16 |
| 짧은 기초 통계 2 : 중심 경향값과 편포(+ 로그/제곱근 변환) (0) | 2024.06.15 |
