수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
중심 경향값에 대한 내용입니다. 내용 자체는 단순 합니다. 평균은 통계를 하지 않아도 많이들 알고 계시고, 분산과 표준편차 또한 많이들 알고 계실 겁니다.
하지만, 이를 왜 알아야하는 가에 대해 알아보려고 합니다.
📌 중심 경향값(central tendency) : 집단을 대표하는 표현
중심 경향값은 분포의 중심을 정의하는 단일 점수를 결정하는 통계 수단입니다.
전체 집단에서 가장 일반적이거나 가장 대표적인 단일 점수를 찾기 위해 사용합니다.
쉽게 말하면 내가 가진 데이터 분포를 하나의 수로 표현하기 위한 방법을 중심 경향값이라고 하는 것입니다.
1. 평균(mean)
우리가 잘 알고있는 평균입니다. 보통은 산술 평균을 사용합니다. 분포의 모든 값들을 더한 후 사례의 수로 나누어 계산합니다.
- 모집단의 평균 : $\mu = \dfrac{\sum X}{N}$
- 표본의 평균 : $\bar{X}(or \ M) = \dfrac{\sum X}{n}$
단점이 있다면 극단치에 취약합니다. X = 4, 6, 8, 8, 9가 있다고 해봅시다. 그럼 평균은 7이 됩니다. 하지만 만약 여기에 100이란 값이 추가 된다면? 평균이 한번에 27이 되버립니다.
2. 중위수(median)
이름 그대로 중앙값입니다. 분포의 중간점으로 분포에서 점수의 50%에 위치하는 측정 척도상의 점입니다.
위의 예시에서 쓰인 X = 4, 6, 8, 8, 9에서 중간에 위치한 값은 8 이므로, 중위수는 8이 됩니다.
중위수는 평균과 다르게 계산이 아주 편합니다. 특별한 계산식 없이도 구할 수 있죠, 또한 극단치에 취약하지도 않습니다. 평균에서 들었던 예시 처럼 값에 100이 더해지더라도 8이 중위수가 됩니다. 하지만 전체 분포에서 오직 중앙에 위치한 값만을 사용하여 중위수를 구하기 때문에 정보의 손실이 큽니다.
3. 최빈값(mode)
최빈값은 빈도가 가장 큰 점수를 말합니다. 가장 일반적인 관찰값이죠. 쉽게 분포에서 가장 많이 나오는 값이라 보면 됩니다.
영어로 mode인 이유는 mode가 프랑스어로 '유행', '가장 흔한 것'이라는 의미이기 때문입니다.
✔︎ 굳이 평균을 사용하는 이유는?
그럼 왜 굳이 극단치에 취약한 평균을 사용할까요?? 계산도 쉽고 극단치에 취약하지 않은 중위수를 사용하면 될텐데 말입니다.
중위수에서 정보 손실도 문제지만, 기초 통계 1편에서 보았고, 앞으로도 보겠지만, 우리가 추출한 표본(샘플)은 모집단에 대한 대표성을 지닌 좋은 샘플로 가정했기 때문입니다. 즉, 평균에 영향을 주는 큰 극단치가 없을 것이라 가정하고 진행하기 때문입니다.
📌 편포(skewed distribution)
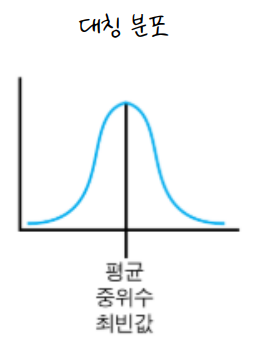
편포란 데이터가 정규성을 보이는 것이 아니라 한쪽으로 치우쳐져 있는 경우를 말합니다. 전통적인 통계는 아래와 같은 대칭 분포의 정규성을 가정하고 분석을 진행합니다. 때문에 많은 경우에 있어서 이 정규성의 가정을 충족하는 것이 중요합니다.
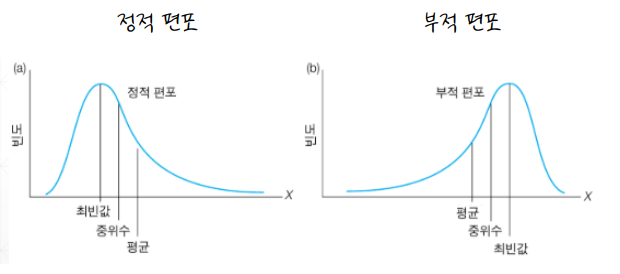
편포의 종류
1. 정적 편포(Positive skew) : 분포의 오른쪽 꼬리가 길게 늘어진 형태. 데이터가 왼쪽에 몰려있음.
2. 부적 편포(Negative skew) : 분포의 왼쪽 꼬리가 길게 늘어진 형태. 데이터가 오른쪽에 몰려있음.
✔︎ 편포의 중요성?
많은 책에서 편포에 따른 평균, 중위수, 최빈값의 차이를 다루고 있습니다. 사실 저는 별로 중요하다고 생각하지 않습니다.(감히... 발언해보자면.. ㅜㅜ) 실제 분석에서 평균을 제외하고 다루지 않는 경우가 많고, 다룬다 하더라고 분석에 있어 크게 중요한 역할을 하지 않습니다.
강조드리고 싶은 부분은 위와 같이 데이터의 분포를 시각화 하는 것이 통계 분석 전 기초 단계라는 것입니다. 이렇게 분포를 확인하는 것 자체만으로 인사이트를 얻을 수 있죠. 예를 들어, 특정 지역 사람들의 임금 데이터가 부적 분포를 띈다고 해봅시다. 이는 해당 지역 주민들이 상대적으로 더 많은 임금을 받는 사람들이 많다는 것을 뜻합니다.
우리가 사용하는 많은 통계적 모델은 데이터의 분포를 반영하기 때문에, 결과를 확인할 수는 있으나 그에 대한 해석과 적용에 문제가 있을 수 있습니다.
위 예처럼 임금 데이터라고 가정할 때, 이를 기준으로 정책을 설계하면 소수의 저임금자들은 정책에서 배제될 수 있는 문제가 생길수도 있는 것입니다.
📌 정규성 확보를 위한 데이터 변환
앞서 많은 통계적 모델이 정규성 가정을 필요로 한다고 하였습니다. 하지만, 실제 우리의 데이터가 정규성을 띄지 못하는 경우가 많습니다.(실제로 정규성 가정 등이 필요 없는 AI가 활발히 발전하는 이유 중 하나..)
그럼에도 우리가 분석을 하려한다면, 데이터의 변환이 필요합니다.
데이터 변환
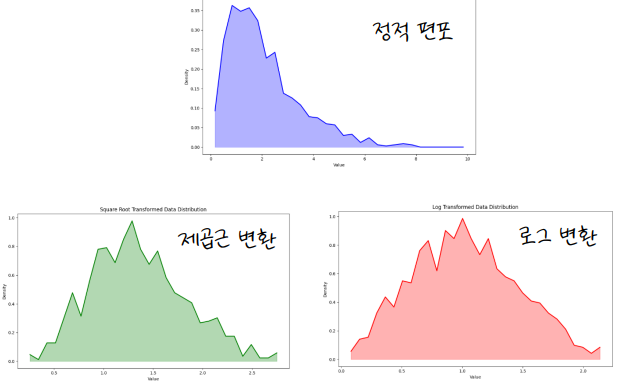
- 로그 변환 : 데이터 값을 그 값의 로그 값으로 대체하는 것. $log(x), ln(x)$
> 편포 데이터를 정규성에 가깝게 만들 수 있다. 또한 매우 큰 값과 작은 값의 차이가 클 때, 스케일을 조정할 수 있다.
- 제곱근 변환 : 데이터 값을 그 값의 제곱근으로 대체하는 것. $\sqrt{x}$
> 이 또한 편포 데이터를 정규성에 가깝게 만들 수 있다.
✔︎ 변환과 해석에 대해
변환하여 정규성을 만족했다고 좋아하는 데는 큰 고민이 필요합니다. 보통 이러한 변환은 예측이 주 목적이 되는 분야에서 많이 사용됩니다. AI와 같은 방법론에서 많이 사용되는데, 해당 분야들은 결국 예측을 얼마나 정확하고 완벽하게 하는 가가 주목적입니다.
하지만 분야에 따라 해석이 중요한 경우가 있습니다.(사회과학 등) 이런 경우 원점수 데이터를 변환한다는 것 자체가 직관적으로 이해하기 어려운 결과를 만들 수 있습니다. 본래 의미가 왜곡되는 것이지요.
예를 들어 '자아 존중감이 높은 사람이 삶의 만족도가 높다.'라고 해석되는 것이 아니라 '자아 존중감의 로그 변환 값이 중간인 사람이 삶의 만족도가 높다.'와 같이 되어 버립니다. 때문에 비모수적 통계 기법을 사용하는 것도 고려해보아야 합니다.
'📊 Statistics for Basic > 기초 통계' 카테고리의 다른 글
| 짧은 기초 통계 4 : z-score(z 점수)와 확률 (1) | 2024.06.26 |
|---|---|
| 짧은 기초 통계 3 : 변산성, 불편 추정량(제약식과 자유도) (1) | 2024.06.16 |
| 짧은 기초 통계 1 : 통계 중요성과 변수 및 척도 (1) | 2024.06.14 |
| 최대 우도 추정법(최대 가능도 추정법)[Maximum Likelihood Estimation] (0) | 2024.04.23 |
| 가능도(Likelihood) vs 확률(Probability) (0) | 2024.04.23 |
중심 경향값에 대한 내용입니다. 내용 자체는 단순 합니다. 평균은 통계를 하지 않아도 많이들 알고 계시고, 분산과 표준편차 또한 많이들 알고 계실 겁니다.
하지만, 이를 왜 알아야하는 가에 대해 알아보려고 합니다.
📌 중심 경향값(central tendency) : 집단을 대표하는 표현
중심 경향값은 분포의 중심을 정의하는 단일 점수를 결정하는 통계 수단입니다.
전체 집단에서 가장 일반적이거나 가장 대표적인 단일 점수를 찾기 위해 사용합니다.
쉽게 말하면 내가 가진 데이터 분포를 하나의 수로 표현하기 위한 방법을 중심 경향값이라고 하는 것입니다.
1. 평균(mean)
우리가 잘 알고있는 평균입니다. 보통은 산술 평균을 사용합니다. 분포의 모든 값들을 더한 후 사례의 수로 나누어 계산합니다.
- 모집단의 평균 : $\mu = \dfrac{\sum X}{N}$
- 표본의 평균 : $\bar{X}(or \ M) = \dfrac{\sum X}{n}$
단점이 있다면 극단치에 취약합니다. X = 4, 6, 8, 8, 9가 있다고 해봅시다. 그럼 평균은 7이 됩니다. 하지만 만약 여기에 100이란 값이 추가 된다면? 평균이 한번에 27이 되버립니다.
2. 중위수(median)
이름 그대로 중앙값입니다. 분포의 중간점으로 분포에서 점수의 50%에 위치하는 측정 척도상의 점입니다.
위의 예시에서 쓰인 X = 4, 6, 8, 8, 9에서 중간에 위치한 값은 8 이므로, 중위수는 8이 됩니다.
중위수는 평균과 다르게 계산이 아주 편합니다. 특별한 계산식 없이도 구할 수 있죠, 또한 극단치에 취약하지도 않습니다. 평균에서 들었던 예시 처럼 값에 100이 더해지더라도 8이 중위수가 됩니다. 하지만 전체 분포에서 오직 중앙에 위치한 값만을 사용하여 중위수를 구하기 때문에 정보의 손실이 큽니다.
3. 최빈값(mode)
최빈값은 빈도가 가장 큰 점수를 말합니다. 가장 일반적인 관찰값이죠. 쉽게 분포에서 가장 많이 나오는 값이라 보면 됩니다.
영어로 mode인 이유는 mode가 프랑스어로 '유행', '가장 흔한 것'이라는 의미이기 때문입니다.
✔︎ 굳이 평균을 사용하는 이유는?
그럼 왜 굳이 극단치에 취약한 평균을 사용할까요?? 계산도 쉽고 극단치에 취약하지 않은 중위수를 사용하면 될텐데 말입니다.
중위수에서 정보 손실도 문제지만, 기초 통계 1편에서 보았고, 앞으로도 보겠지만, 우리가 추출한 표본(샘플)은 모집단에 대한 대표성을 지닌 좋은 샘플로 가정했기 때문입니다. 즉, 평균에 영향을 주는 큰 극단치가 없을 것이라 가정하고 진행하기 때문입니다.
📌 편포(skewed distribution)
편포란 데이터가 정규성을 보이는 것이 아니라 한쪽으로 치우쳐져 있는 경우를 말합니다. 전통적인 통계는 아래와 같은 대칭 분포의 정규성을 가정하고 분석을 진행합니다. 때문에 많은 경우에 있어서 이 정규성의 가정을 충족하는 것이 중요합니다.

편포의 종류
1. 정적 편포(Positive skew) : 분포의 오른쪽 꼬리가 길게 늘어진 형태. 데이터가 왼쪽에 몰려있음.
2. 부적 편포(Negative skew) : 분포의 왼쪽 꼬리가 길게 늘어진 형태. 데이터가 오른쪽에 몰려있음.

✔︎ 편포의 중요성?
많은 책에서 편포에 따른 평균, 중위수, 최빈값의 차이를 다루고 있습니다. 사실 저는 별로 중요하다고 생각하지 않습니다.(감히... 발언해보자면.. ㅜㅜ) 실제 분석에서 평균을 제외하고 다루지 않는 경우가 많고, 다룬다 하더라고 분석에 있어 크게 중요한 역할을 하지 않습니다.
강조드리고 싶은 부분은 위와 같이 데이터의 분포를 시각화 하는 것이 통계 분석 전 기초 단계라는 것입니다. 이렇게 분포를 확인하는 것 자체만으로 인사이트를 얻을 수 있죠. 예를 들어, 특정 지역 사람들의 임금 데이터가 부적 분포를 띈다고 해봅시다. 이는 해당 지역 주민들이 상대적으로 더 많은 임금을 받는 사람들이 많다는 것을 뜻합니다.
우리가 사용하는 많은 통계적 모델은 데이터의 분포를 반영하기 때문에, 결과를 확인할 수는 있으나 그에 대한 해석과 적용에 문제가 있을 수 있습니다.
위 예처럼 임금 데이터라고 가정할 때, 이를 기준으로 정책을 설계하면 소수의 저임금자들은 정책에서 배제될 수 있는 문제가 생길수도 있는 것입니다.
📌 정규성 확보를 위한 데이터 변환
앞서 많은 통계적 모델이 정규성 가정을 필요로 한다고 하였습니다. 하지만, 실제 우리의 데이터가 정규성을 띄지 못하는 경우가 많습니다.(실제로 정규성 가정 등이 필요 없는 AI가 활발히 발전하는 이유 중 하나..)
그럼에도 우리가 분석을 하려한다면, 데이터의 변환이 필요합니다.
데이터 변환
- 로그 변환 : 데이터 값을 그 값의 로그 값으로 대체하는 것. $log(x), ln(x)$
> 편포 데이터를 정규성에 가깝게 만들 수 있다. 또한 매우 큰 값과 작은 값의 차이가 클 때, 스케일을 조정할 수 있다.
- 제곱근 변환 : 데이터 값을 그 값의 제곱근으로 대체하는 것. $\sqrt{x}$
> 이 또한 편포 데이터를 정규성에 가깝게 만들 수 있다.

✔︎ 변환과 해석에 대해
변환하여 정규성을 만족했다고 좋아하는 데는 큰 고민이 필요합니다. 보통 이러한 변환은 예측이 주 목적이 되는 분야에서 많이 사용됩니다. AI와 같은 방법론에서 많이 사용되는데, 해당 분야들은 결국 예측을 얼마나 정확하고 완벽하게 하는 가가 주목적입니다.
하지만 분야에 따라 해석이 중요한 경우가 있습니다.(사회과학 등) 이런 경우 원점수 데이터를 변환한다는 것 자체가 직관적으로 이해하기 어려운 결과를 만들 수 있습니다. 본래 의미가 왜곡되는 것이지요.
예를 들어 '자아 존중감이 높은 사람이 삶의 만족도가 높다.'라고 해석되는 것이 아니라 '자아 존중감의 로그 변환 값이 중간인 사람이 삶의 만족도가 높다.'와 같이 되어 버립니다. 때문에 비모수적 통계 기법을 사용하는 것도 고려해보아야 합니다.
'📊 Statistics for Basic > 기초 통계' 카테고리의 다른 글
| 짧은 기초 통계 4 : z-score(z 점수)와 확률 (1) | 2024.06.26 |
|---|---|
| 짧은 기초 통계 3 : 변산성, 불편 추정량(제약식과 자유도) (1) | 2024.06.16 |
| 짧은 기초 통계 1 : 통계 중요성과 변수 및 척도 (1) | 2024.06.14 |
| 최대 우도 추정법(최대 가능도 추정법)[Maximum Likelihood Estimation] (0) | 2024.04.23 |
| 가능도(Likelihood) vs 확률(Probability) (0) | 2024.04.23 |
