수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 로지스틱 회귀(Logistic Regression)
만약, 특정 사람이 외향적인지를 분류한다고 해봅시다.(외향 vs 내향이 아닙니다. 외향 Yes vs No 입니다)
반응 변수 명을 $x_1$라고 하면 두 개의 범주 Yes or No 가 있을 것입니다.
로지스틱 회귀는 반응 변수 Y를 직접 모델링하지 않고 Y가 특정 범주에 속하는 확률을 모델링 합니다.
추가적인 예로 일주일에 외출 횟수를 설명 변수로 사용하고, 변수 명을 out이라고 하였을 때, out에 대한 외향적일 확률을 다음과 같이 표시할 수 있습니다. Pr(Ex = Yes|out)이 값을 줄여서 p(out)라고 하고, 범위는 0~1입니다.
이를 이용해 임의의 주어진 out에 대해 Ex를 예측 할 수 있습니다. 예를 들어 p(out) > 0.5인 사람은 Ex = Yes, 그 반대는 No라고 할 수 있겠죠
◼️ 로지스틱 모델
만약 위 예시를 일반 선형회귀모델에 적용 한다면. $( p(X) = beta0 + beta1 * X )$ 문제가 발생합니다.
위 글 처럼, 예측 확률이 0보다 아래인 음수가 되어버리거나, 1보다 넘어버립니다. 하지만 위에서 우리는 범위를 0~1이라고 하였죠. 어떠한 일이 일어날 확률이 100%를 넘거나 0%아래로 될 수는 없으니까요.
위 문제를 해결하기 위해 모든 X 값에 대해 0~1사이의 값을 Y로 나타낼 수 있는 함수를 모델링 해야 합니다.
이를 위해 로지스틱 회귀에서는 아래와 같은 함수를 이용합니다.
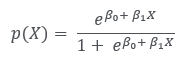
이러한 모델의 적합을 위해서는 최대가능도라고 하는 방안을 사용합니다. 또한 위 식은 아래와 같이도 표현 가능합니다.
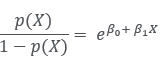
여기서 p(X)/1-p(X)를 우리는 공산(odds)이라고 합니다.
◼️ 공산
: 항상 0과 무한대 사이의 수를 가지며, 0에 가까우면 분모의 수가 크다는 것을 의미하니 p(X)는 작은 값일 것입니다. 즉 0에 가까우면 예시에서 외향적일 확률이 매우 낮고, 반대로 무한대에 가깝다면 크다는 것을 의미하겠죠.
위 식의 양변에 로그를 취해봅시다.
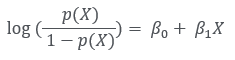
자연상수 e가 자연스럽게 빠져나와 지수인 $\beta_0 + \beta_1 X$에 대한 식이 됩니다. 어디서 많이 봤던 식이죠? 본래 선형회귀 식인
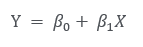
와 상당히 유사합니다.
로그를 취한 (2)의 식에서 좌변을 로그 공산(log-odds) 또는 로짓(logit)이라고 합니다.
쉽게 설명하면 로그 공산은 어떤 사건이 발생활 확률(p(X))와 발생하지 않을 확률(1-p(X))의 로그 비율을 나타내는 개념입니다.
선형회귀모델을 보면, beta1은 X의 한 유닛 증가와 관련하여 Y의 평균 변화를 제공하죠. 로지스틱 회귀모델에서 X의 한 유닛 증가는 로그 공산을 beta1만큼 변화시킵니다.
◼️ 회귀계수 추정
회귀계수의 추정은 일반선형회귀의 경우 최소제곱법을 사용하여 구했었죠. 로지스틱 회귀모델에서는 주로 최대가능도를 사용하여 구합니다. 이에 대한 근거는 예로 다시 봅시다.
식 (2)를 사용하여 예측한 개인의 외향일 확률이 관측된 사람들의 외향인 상태와 가능하면 가깝도록 $\beta_0$과 $\beta_1$을 추정하려고 하는 것입니다.
즉, 추정치 $\beta_0$ 과 $\beta_1$ 을 찾고자 하는데 이 추정치를 식 (2)의 p(X)에 대입하면 외향적인 사람들에 대해서는 1에 가깝고 외향적이지 않은 사람들에 대해서는 0에 가까운 값을 도출하는 겁니다.
이를 함수로 표현하면
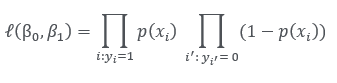
(3)에 대한 자세한 설명은 다음 포스팅에서 다루겠습니다.
📌 다중 로지스틱 회귀
앞서 다중선형회귀와 같은 맥락으로 이루어집니다.
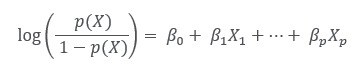
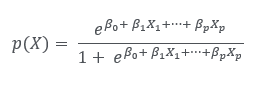
와 같고 똑같이 최대가능도 방법을 사용하여 beta값들을 추정합니다.
'📊 Statistics for Basic > 통계 학습(Statistical learning)' 카테고리의 다른 글
| 편향과 분산 : trade off와 MSE의 관계 (0) | 2023.10.12 |
|---|---|
| Validation set와 MSE : Validation set를 사용하는 이유 (1) | 2023.10.12 |
| 전진 단계적 선택(Forward stepwise), 후진 단계적 선택(Backward stepwise) (0) | 2023.10.12 |
| Leave-one-out 교차 검증과 K-fold 교차 검증 (0) | 2023.10.12 |
| 다중 선형회귀 (0) | 2023.10.12 |