수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
앞서 단순 선형 포스팅을 확인해주세요.
단순 선형회귀
📌 단순 선형회귀 하나의 설명변수 X에 기초하여 양적변수 Y를 예측합니다. 이 기법은 X와 Y 사이 선형 상관관계가 있다고 가정하며 아래의 식으로 나타낼 수 있습니다. 위 식을 x에 대한 Y의 회
datanovice.tistory.com
📌 다중 선형회귀
단순선형회귀는 단일 설명변수(x1)을 기반으로 반응변수를 예측하는 기법입니다.
하지만 실제로 하나의 변수만으로 예측이 가능할까요? 실제로는 하나보다 많은 설명변수가 필요합니다.
예를 들어, 내일 비올 확률을 계산해봅시다. 단순히 습도만 가지고 예측하기는 어렵죠. 습도, 바람, 고도 등 많은 설명변수가 필요합니다.
그렇다면 각각의 설명변수를 이용해 세 개의 단순선형회귀를 만들어서 사용하면 어떨까요?
- 비올 확률 = intercept + beta1 * 습도
- 비올 확률 = intercept + beta2 * 바람
- 비올 확률 = intercept + beta3 * 고도
이렇게 단순회귀식을 만들었다고 생각해봅시다.
하지만 가시적으로 보았을 때도 알 수 있듯 이는 만족할만한 방정식이 되지 못합니다.
서로 다른 설명변수들의 상관을 무시하고 독립적으로 보기 때문에 현실적으로 실현되기 어려운 식입니다.
때문에 여러 단순회귀식이 아닌 이를 확장한 다중선형회귀모델을 사용할 것입니다.
모델은 아래와 같습니다. (설명변수가 p개 있을 때)
$$
Y =\beta_0 + \beta_1 X_1 + ... + \beta_p X_p + \epsilon
$$
위의 예를 적용해 보면
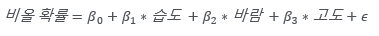
이런 식이 완성됩니다.
◼️ 계수 추정
단순선형회귀와 같이 회귀 계수$(\beta_0, \beta_1, ... , \beta_p)$는 알려지지 않은 값이며 우리가 추정해야 합니다.
추정을 통해 회귀식을 만들면 아래와 같습니다.
$$
\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + ... + \hat{\beta}_p x_p
$$
파라미터들은 앞서 단순선형회귀에서 살펴보았 듯 동일하게 최소제곱법을 사용하여 추정할 수 있다.
즉, $\beta_0, \beta_1, ... , \beta_p$는 잔차제곱합(sum of squared residuals)을 최소화하도록 선택됩니다.
(이해가 어렵다면 꼭 단순선형회귀 포스팅을 봐주세요!, 잔차제곱합의 더욱 상세하고 쉬운 설명은 따로 포스팅할 예정입니다.)
$$
\begin{align}
RSS &= \sum_{i=1}^n (y_i - \hat{y}_i)^2
&= \sum{i=1}^n (y_i -(\hat{\beta}_0 + \hat{\beta}_1 x_1 + ... + \hat{\beta}_p x_p))
\end{align}
$$
식의 윗 부분이 잔차제곱합의 식입니다. 이 식에 위에 보여드린 회귀식을 대입하여 풀어쓴 것이 아래 부분의 식입니다.
해당 식을 최소화하는 계수를 찾는 것입니다.
단순선형회귀와는 달리 다중선형회귀추정값은 복잡한 형태를 지니며, 행렬대수를 사용하여 표현할 수 있습니다.
그리고 요즘은 통계 프로그램을 이용하여 빠르게 파라미터 계수를 추정할 수 있습니다.
정말 간단하게 다중선형회귀에 대해 알아보았습니다.
뒤 포스팅은 다중선형회귀에 있어서 중요한 질문들에 대해 알아보려고 합니다.
'📊 Statistics for Basic > 통계 학습(Statistical learning)' 카테고리의 다른 글
| Validation set와 MSE : Validation set를 사용하는 이유 (1) | 2023.10.12 |
|---|---|
| 로지스틱 회귀(Logistic Regression) (1) | 2023.10.12 |
| 전진 단계적 선택(Forward stepwise), 후진 단계적 선택(Backward stepwise) (0) | 2023.10.12 |
| Leave-one-out 교차 검증과 K-fold 교차 검증 (0) | 2023.10.12 |
| 단순 선형회귀 (0) | 2023.10.12 |
앞서 단순 선형 포스팅을 확인해주세요.
단순 선형회귀
📌 단순 선형회귀 하나의 설명변수 X에 기초하여 양적변수 Y를 예측합니다. 이 기법은 X와 Y 사이 선형 상관관계가 있다고 가정하며 아래의 식으로 나타낼 수 있습니다. 위 식을 x에 대한 Y의 회
datanovice.tistory.com
📌 다중 선형회귀
단순선형회귀는 단일 설명변수(x1)을 기반으로 반응변수를 예측하는 기법입니다.
하지만 실제로 하나의 변수만으로 예측이 가능할까요? 실제로는 하나보다 많은 설명변수가 필요합니다.
예를 들어, 내일 비올 확률을 계산해봅시다. 단순히 습도만 가지고 예측하기는 어렵죠. 습도, 바람, 고도 등 많은 설명변수가 필요합니다.
그렇다면 각각의 설명변수를 이용해 세 개의 단순선형회귀를 만들어서 사용하면 어떨까요?
- 비올 확률 = intercept + beta1 * 습도
- 비올 확률 = intercept + beta2 * 바람
- 비올 확률 = intercept + beta3 * 고도
이렇게 단순회귀식을 만들었다고 생각해봅시다.
하지만 가시적으로 보았을 때도 알 수 있듯 이는 만족할만한 방정식이 되지 못합니다.
서로 다른 설명변수들의 상관을 무시하고 독립적으로 보기 때문에 현실적으로 실현되기 어려운 식입니다.
때문에 여러 단순회귀식이 아닌 이를 확장한 다중선형회귀모델을 사용할 것입니다.
모델은 아래와 같습니다. (설명변수가 p개 있을 때)
$$
Y =\beta_0 + \beta_1 X_1 + ... + \beta_p X_p + \epsilon
$$
위의 예를 적용해 보면
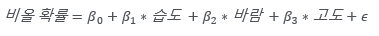
이런 식이 완성됩니다.
◼️ 계수 추정
단순선형회귀와 같이 회귀 계수$(\beta_0, \beta_1, ... , \beta_p)$는 알려지지 않은 값이며 우리가 추정해야 합니다.
추정을 통해 회귀식을 만들면 아래와 같습니다.
$$
\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + ... + \hat{\beta}_p x_p
$$
파라미터들은 앞서 단순선형회귀에서 살펴보았 듯 동일하게 최소제곱법을 사용하여 추정할 수 있다.
즉, $\beta_0, \beta_1, ... , \beta_p$는 잔차제곱합(sum of squared residuals)을 최소화하도록 선택됩니다.
(이해가 어렵다면 꼭 단순선형회귀 포스팅을 봐주세요!, 잔차제곱합의 더욱 상세하고 쉬운 설명은 따로 포스팅할 예정입니다.)
$$
\begin{align}
RSS &= \sum_{i=1}^n (y_i - \hat{y}_i)^2
&= \sum{i=1}^n (y_i -(\hat{\beta}_0 + \hat{\beta}_1 x_1 + ... + \hat{\beta}_p x_p))
\end{align}
$$
식의 윗 부분이 잔차제곱합의 식입니다. 이 식에 위에 보여드린 회귀식을 대입하여 풀어쓴 것이 아래 부분의 식입니다.
해당 식을 최소화하는 계수를 찾는 것입니다.
단순선형회귀와는 달리 다중선형회귀추정값은 복잡한 형태를 지니며, 행렬대수를 사용하여 표현할 수 있습니다.
그리고 요즘은 통계 프로그램을 이용하여 빠르게 파라미터 계수를 추정할 수 있습니다.
정말 간단하게 다중선형회귀에 대해 알아보았습니다.
뒤 포스팅은 다중선형회귀에 있어서 중요한 질문들에 대해 알아보려고 합니다.
'📊 Statistics for Basic > 통계 학습(Statistical learning)' 카테고리의 다른 글
| Validation set와 MSE : Validation set를 사용하는 이유 (1) | 2023.10.12 |
|---|---|
| 로지스틱 회귀(Logistic Regression) (1) | 2023.10.12 |
| 전진 단계적 선택(Forward stepwise), 후진 단계적 선택(Backward stepwise) (0) | 2023.10.12 |
| Leave-one-out 교차 검증과 K-fold 교차 검증 (0) | 2023.10.12 |
| 단순 선형회귀 (0) | 2023.10.12 |