수식이 나오지 않는다면 새로고침(F5)을 해주세요
모바일은 수식이 나오지 않습니다.
📌 NN(Neural network)
뉴럴 네트워크는 통계적인 모델링이나 패턴 인식에 적용되는 기계 학습(Machine learning)중 하나입니다.
기본 원리는 우리의 뉴런과 같습니다. 뉴런의 작동방식에 영감을 받아 만들어진 모델로, 여러 계층의 뉴런들이 서로 연결되어 입력(input)에서 출력(output)으로의 복잡한 mapping을 학습합니다.
각 뉴런은 입력을 받아 가중치를 적용하고 활성화 함수를 통과하여 이의 결과를 다음 뉴런으로 전달합니다.
신경망 구조로서 뉴럴 네트워크를 입력 계층, 은닉 계층, 출력 계층으로 구성됩니다. 각 계층은 여러 뉴런으로 이루어져 있고, 이 신경망의 깊이(은닉 층의 개수), 그리고 너비(뉴런의 개수)를 결정하는 것이 point라고 할 수 있습니다.


◾ Feed Forward Neural Network
순방향 신경망(feed forward neural network)는 가장 기본적이고 일반적인 형태의 인공 신경망입니다. 입력층 > 은닉층 > 출력층으로 단방향으로 흐르는 구조입니다.
각 노드는 입력과 가중치의 선형 조합을 계산하고, 활성화 함수를 통해 출력을 생성합니다.
가중치는 손실함수를 통해 예측, 실제값 사이의 오차를 계산하고, 역전파 알고리즘을 통해 오차를 감소시키기 위해 가중치를 조정합니다.
아마 Deep neural network라고 들어보셨을 겁니다. 이는 은닉층의 개수가 두 개 이상일 때를 말합니다.(Deep learning) 은닉층의 개수가 많아질수록 모델을 깊고, 해석이 어려워집니다.
앞으로 보여드릴 여러 식들의 표현에 대한 설명입니다. 참고해 주세요.
| $w_{ji}^{n}$(weight) | n번째 은닉층의 $i$번째 노드에서 $n+1$ or 출력층의 $k$번째 노드로의 가중치 |
| $w_{j0}^n$(bias) | 은닉층 or 출력층의 $j$번째 노드의 편향 |
| $h, \sigma$(actication functions) | 각각 은닉층, 출력층의 활성화 함수 |
| $a_j$(activation) | 은닉층의 $j$번째 노드에 대한 활성화 값 |
| $z_j = h(a_j)$(hidden unit) | 은닉층의 $j$번째 노드의 출력. 활성화 함수를 적용한 활성화 값 |
아래는 대중적으로 사용하는 활성화 함수입니다.
| sigmoid | $h(a) = \dfrac{e^a}{1+e^a}$ | $h'(a) = h(a)(1-h(a))$ |
| hyperbolic tangent | $h(a) = \dfrac{e^a - e^{-a}}{e^a + e^{-a}}$ | $h'(a) = 1-h^2(a)$ |
| rectifiered linear unit(ReLU) | $h(a) = \max(0,a)$ | $h'(a) = I(a >0)$ |
◾ cost or loss function and optimization
뉴럴 네트워크에서는 손실 함수와 최적화 알고리즘이 중요한 역할을 합니다.
손실 함수 : 모델의 출력과 실제 값 사이의 차이를 측정하고 이를 최소화하여 모델이 원하는 결과를 더 정확하게 예측하도록 하기 위함. 일반적으로 다른 모델에서도 많이 쓰이는 평균 제곱 오차(MSE) 혹은 cross entropy 등 여러 손실 함수를 사용
최적화 : 손실 함수를 최소화하는 최적의 매개변수(가중치 및 편향)를 찾는 과정. 역전파 알고리즘이 사용되어 모델의 손실이 최소가 되는 방향으로 매개변수를 업데이트한다. 대표적으로 확률적 경사하강법, 모멘텀 최적화, Adagrad, Adam 등이 사용됩니다.
이러한 손실함수, 최적화 알고리즘의 선택에 따라 모델의 학습 성능과 수렴 속도에 큰 영향을 미친다. 적합한 알고리즘을 선택하는 것이 중요.
1️⃣ 회귀에서
회귀에서 쓰이는 목적함수(손실함수)로는 평균 제곱 오차(MSE)가 있습니다. 각 예측값 $\textbf{f}(\textbf{x}_i, \textbf{w})$과 실제값 $\textbf{t}_i$간의 차이 제곱을 모든 데이터 포인트에 더한 것의 반을 최소화하는 방향으로
$$
E(\textbf{w}) = \dfrac12 \sum_{i=1}^N ||\textbf{t}_i - \textbf{f}(\textbf{x}_i, \textbf{w})||^2
$$
2️⃣ 이진 분류에서
이진 분류에서 쓰이는 목적함수(손실함수)로는 로지스틱 회귀의 손실함수로서, cross entropy loss를 최소화하는 방향으로. 각 클래스에 대한 예측 확률과 실제 레이블 간의 차이를 고려한다.
$$
\begin{align}
L &= \prod_{i=1}^N(f(\textbf{x}_i, \textbf{w})^{t_i}(1-f(\textbf{x}_i, \textbf{w}))^{1-t_i}
\\ l &= \sum_{i=1}^N [t_i \log f(\textbf{x}_i, \textbf{w}) + (1-t_i) \log(1-f(\textbf{x}_i, \textbf{w}))]
\\ E(\textbf{w}) &= -\sum_{i=1}^N [t_i \log f(\textbf{x}_i, \textbf{w}) + (1-t_i) \log(1-f(\textbf{x}_i, \textbf{w}))]
\end{align}
$$
3️⃣ 다중 분류에서
다중 분류에서는 다중 클래스 로지스틱 회귀의 손실함수로서, cross entropy loss를 최소화하는 방향으로.
$$
\begin{align}
L &= \prod_{i=1}^N\prod_{g=1}^G(f_g(\textbf{x}_i, \textbf{w}))^{t_gi}
\\ l &= \sum_{i=1}^N\sum_{g=1}^G[t_{gi} \log f_g(\textbf{x}_i, \textbf{w})]
\\ E(\textbf{w}) &= -\sum_{i=1}^N\sum_{g=1}^G[t_{gi} \log f_g(\textbf{x}_i, \textbf{w})]
\end{align}
$$
◾ 최적화 : 경사하강법(batch, on-line method)
최적화 알고리즘으로 사용하는 경사하강법에서 batch method와 on-line method가 있는데
배치 방법은 전체 훈련 데이터 세트를 사용하여 한 번에 매개변수를 업데이트하는 방법이다. 즉, 손실 함수의 그레디언트를 계산하고 전체 데이터에 대해 업데이트한다. 안정적이지만.. 데이터가 클수록 계산비용이 높다.
$$
\textbf{w}^{r+1} = \textbf{w}^r - \eta \nabla E(\textbf{w}^r)
$$
on-line 방법은 각 훈련 데이터 포인트에 대해 매개변수를 업데이트한다(전체 한 번에 x). 데이터를 한 번에 하나씩 처리하며 매개변수를 조정한다.
$$
\textbf{w}^{r+1} = \textbf{w}^r -\eta \nabla E_i(\textbf{w}^r)
$$
여기서 $\eta$가 아시겠지만 경사하강법의 learning rate로서 조절해줘야 하는 튜닝 파라미터이다.
◾ 역전파 알고리즘
앞서 계속해서 역전파 알고리즘에 대해서 설명하였었습니다. 한번 알아봅시다.
손실 함수의 그래디언트를 계산하여 가중치를 조정하여 모델을 학습시킵니다.
주어진 손실함수가 아래와 같다고 할 때
$$
E(\textbf{w}) = \sum_{i=1}^N E_n(\textbf{w})
$$
여기서 $E_n(\textbf{w})$는 각각의 데이터 포인트 $n$에 대한 손실함수이며 다음과 같습니다.($t$가 실제값)
$$
E_n(\textbf{w}) = \dfrac12 \sum_k(y_{nk} - t_{nk})^2
$$
아래가 핵심인데 위에서부터 차례대로
1번째 은닉층의 $i$번째 노드(or 입력층)에서 다음은닉층의 $j$번째 노드로의 가중치의 그래디언트.
2번째 은닉층의 $j$번째 노드에서 출력층의 $k$번째 노드로의 가중치의 그래디언트.
$\delta_k$ : 출력층 노드의 오차 신호
$\delta_j$ : 은닉층 노드의 오차 신호
$a_j^1 = \sum_{i=1}^D w_{ji}^1 x_i + w_{j0}^1, \ a_k^2 = \sum_{j=1}^M w_{kj}^2 h(a_j^1) + w_{k0}^2$
$$
\begin{align}
\dfrac{\partial E_n}{\partial w_{ji}^1} &= \delta_j x_i
\\ \dfrac{\partial E_n}{\partial w_{kj}^2} &= \delta_k z_j
\\ \delta_k &= (y_k - t_k)\sigma'(a_k^2)
\\ \delta_j &= \sum_k (y_k - t_k)\sigma' (a_k^2) w_{kj}^2 h'(a_j^1)
\\ &= \sum_k w_{kj}^2 \delta_k h'(a_j^1)
\end{align}
$$
📌 예제
예를 들어 뉴럴 네트워크에 대해 계산해봅시다.

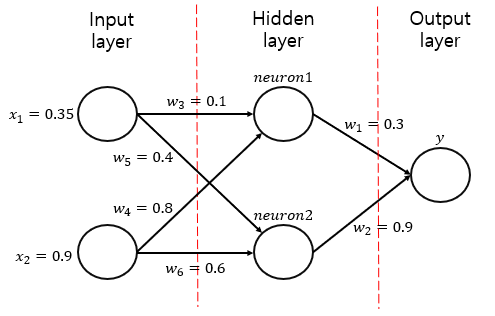
위와 같이 가중치를 계산했고 입력값이 있습니다. 또한 우리는 sigmoid 활성화 함수를 이용할 것이고 학습률 $\eta =1$을 사용하겠습니다.
1️⃣ feed forward. calculate neuron1, neuron2, y
우선 전체적인 y의 식은 아래와 같을 겁니다.
$$
y= h_1(w_1h(w_3x_1 + w_4x_2) + w_2h(w_5x_1 + w_6x_2))
$$
Input 값에 가중치를 더한 것을 합한 것에 활성화함수를 적용하고 이에 또다시 y로 가는 가중치를 적용해 활성화 함수를 적용하는 것입니다.
$$
\begin{align}
neuron1 &= h(w_3x_1 + w_4x_2) = h(0.35 \times 0.1 + 0.9 \times 0.8)
\\ &=h(0.755) = \dfrac{e^{0.755}}{1+ e^{0.755}} = 0.68
\\ neuron2 &= h(w_5x_1 + w_6x_2) = h(0.4 \times 0.35 + 0.9 \times 0.6)
\\ &=h(0.68) = \dfrac{e^{0.68}}{1+ e^{0.68}} = 0.6637
\\ y &= h(w_1\times 0.68 + w_2 \times 0.6637)
\\ &= h(0.80133) =\dfrac{e^{0.80133}}{1+ e^{0.80133}}= 0.69
\end{align}
$$
2️⃣ 역전파 (target = 0.5) 알고리즘(신경망 가중치 업데이트)
◾ Output error 계산(출력층이 하나라 쉽게 계산 가능)
$$
\delta = (y-t)y(1-y) = (0.69-0.5)0.69(1-0.69) = 0.0406
$$
◾ 새로운 가중치 업데이트(for output layer)
$$
w_1^+ = w_1 - \eta(\delta \times input) = 0.3 - (0.0406 \times 0.68) = 0.272392
\\ w_2^+ = w_2 - \eta(\delta \times input) = 0.9 - (0.0406 \times 0.6637) = 0.87305
$$
◾ Hidden layer error 계산
$$
\begin{align}
\delta_1 &= \delta \times w_1 \times z_1(1-z_1) = 0.0406 \times 0.272392 \times \dfrac{e^{0.755}}{1+ e^{0.755}}(1-\dfrac{e^{0.755}}{1+ e^{0.755}})
\\ &= 2.406 \times10^{-3}
\\ \delta_2 &= \delta \times w_2 \times z_2(1-z_2) = 0.0406 \times 0.87305 \times \dfrac{e^{0.68}}{1+ e^{0.68}}(1-\dfrac{e^{0.68}}{1+ e^{0.68}})
\\ &= 7.916 \times10^{-3}
\end{align}
$$
◾ 새로운 가중치 업데이트(for hidden layer)
$$
\begin{align}
w_3^+ &= 0.1 - (2.406 \times 10^{-3} \times 0.35) = 0.09916
\\ w_4^+ &= 0.8 - (2.406 \times 10^{-3} \times 0.9) = 0.7978
\\ w_5^+ &= 0.4 - (7.916 \times 10^{-3} \times 0.35) = 0.3972
\\ w_6^+ &= 0.6 - (7.916 \times 10^{-3} \times 0.9) = 0.5928
\end{align}
$$
3️⃣ 다시 한번 neuron1, neuron2, y 값 확인... 이를 설정값까지 반복..
생각보다 복잡하긴 합니다. y값이 증가하고 노드가 증가하고 은닉층이 증가할 때마다 식이 급격히 늘어나게 됩니다. 그러니 우리는 프로그램에 맡깁시다..!
'👨💻 Deep Learning > Deep learning' 카테고리의 다른 글
| Tensorflow? 텐서플로우? (0) | 2024.08.01 |
|---|---|
| 활성화 함수들의 정의와 활용 : 시그모이드, 소프트맥스, ReLU, Leakly ReLU (0) | 2024.03.26 |
| 경사 하강법 최적화 알고리즘 : Momentum method, AdaGrab, RMSProp, Adam (0) | 2023.12.14 |
| 드롭 아웃(Drop out)과 정규화(Regularization) (0) | 2023.12.13 |
| 경사 하강법 : 배치, 확률적, 미니 배치 경사하강법(Batch, Stochastic, Mini Batch) (0) | 2023.12.13 |
